题目内容
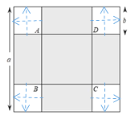
【题目】有一个边长为a的大正方形和四个边长为b的全等的小正方形(其中a>2b),按如图方式摆放,并顺次连接四个小正方形落入大正方形内部的顶点,得到四边形ABCD.
下面有四种说法:
①阴影部分周长为4a;
②阴影部分面积为(a+2b)(a-2b);
③四边形ABCD周长为8a-4b;
④四边形ABCD的面积为a24ab4b2.
所有合理说法的序号是____.

【答案】①②④.
【解析】
①利用平移法即可发现阴影部分的周长=大正方形的周长,计算大正方形的周长即可;
②用大正方形的面积减去四个小正方形的面积即可;
③先证出四边形ABCD是正方形,然后计算出ABCD的边长,即可计算它的周长;
④根据③中的边长求面积即可.
解:①如下图所示:利用平移法可发现:阴影部分的周长=大正方形的周长=4a,
故①正确;
②阴影部分的面积=大正方形的面积-四个小正方形的面积= a2b2=(a+2b)(a-2b)
故②正确;
③由图可知:AB=a-2b,AD=a-2b,∠BAD=90°
∴四边形ABCD是正方形,
∴四边形ABCD的周长为:4(a-2b)=4a-8b
故③错误;
④正方形ABCD的面积为:(a-2b)2= a24ab4b2
故④正确.
故答案为:①②④.

练习册系列答案
相关题目