题目内容
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
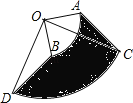
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
【答案】(1)将△AOC绕点O顺时针旋转90°可以得到△BOD;(2)![]() π(cm2).
π(cm2).
【解析】
试题分析:(1)根据旋转的定义求解;
(2)先利用弧长公式计算出OA=2,再根据旋转的性质得到△AOC≌△BOD,则S△AOC=S△BOD,接着根据S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分得到S阴影部分=S扇形COD﹣S扇形AOB,然后利用扇形的面积公式计算即可.
解:(1)∵扇形OAB和扇形OCD的圆心角都是90°,
∴OA=OB,OC=OD,∠AOB=∠COD=90°,
∴将△AOC绕点O顺时针旋转90°可以得到△BOD;
(2)∵![]() =π,
=π,
∴OA=2,
∵△AOC绕点O顺时针旋转90°可以得到△BOD,
∴△AOC≌△BOD,
∴S△AOC=S△BOD,
∵S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分,
∴S阴影部分=S扇形COD﹣S扇形AOB=![]() ﹣
﹣![]() =
=![]() π(cm2).
π(cm2).

练习册系列答案
相关题目