[题目]阅读下文.寻找规律．计算:(1﹣x)(1+x)=1﹣x2.(1﹣x)(1+x+x2)=1﹣x3.(1﹣x)(1+x+x2+x3)=1﹣x4-．(1)观察上式.并猜想:(1﹣x)(1+x+x2+-+xn)= ．(2)根据你的猜想.计算:1+3+32+33-+3n= ．(其中n是正整数) 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】阅读下文，寻找规律．

计算：（1﹣x）（1+x）=1﹣x2，（1﹣x）（1+x+x2）=1﹣x3，（1﹣x）（1+x+x2+x3）=1﹣x4…．

（1）观察上式，并猜想：（1﹣x）（1+x+x2+…+xn）= ．

（2）根据你的猜想，计算：1+3+32+33…+3n= ．（其中n是正整数）

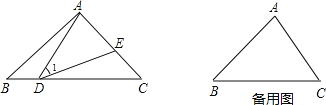
【答案】（1）1﹣xn+1，（2）﹣．

【解析】

试题分析：（1）归纳总结得到一般性规律，写出即可；

（2）原式变形后，利用得出的规律计算即可得到结果．

解：解：（1）（1﹣x）（1+x+x2+…+xn）=1﹣xn+1；

（2）1+3+32+…+3n=﹣（1﹣3）（1+3+32+33…+3n）=﹣．

故答案为：（1）1﹣xn+1，

（2）﹣．

练习册系列答案

1加1阅读好卷系列答案

A. 0 B. 1 C. 2 D. 3

（1）∠B= 度．

（2）如图1，若点D在斜边BC上，DM垂直平分BE，垂足为M．求证：BD=AE；

（3）如图2，过点B作BF⊥CE，交CE的延长线与点F．若CE=6，求△BEC的面积．

（1）由题设条件，请写出三个正确结论：（要求不再添加其他字母和辅助线，找结论过程中添加的字母和辅助线不能出现在结论中，不必证明）

答：结论一：；

结论二：；

结论三：．

（2）若∠B=45°，BC=2，当点D在BC上运动时（点D不与B、C重合），

①求CE的最大值；

②若△ADE是等腰三角形，求此时BD的长．

（注意：在第（2）的求解过程中，若有运用（1）中得出的结论，须加以证明）

（1）将△AOC经过怎样的图形变换可以得到△BOD？

（2）若的长为πcm，OD=3cm，求图中阴影部分的面积是多少？

试题分类