题目内容
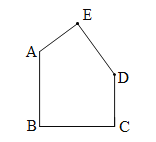
【题目】如图:五边形ABCDE中,AB∥CD,BC⊥AB,AB=BC=8,CD=5.
(1)说明∠A,∠E,∠D之间的数量关系;
(2)平移五边形ABCDE,使D点移动到C点,画出平移后的五边形A'B'C'CE',并求出顺次连接A、A'、E'、C、D、E、A各点所围成的图形的面积;
(3)在∠BAE和∠E'CD的内部取一点F,使∠EAF=![]() ∠EAB,∠FCE'=
∠EAB,∠FCE'=![]() ∠DCE' ,求∠AFC与∠AED之间的数量关系.
∠DCE' ,求∠AFC与∠AED之间的数量关系.
【答案】(1)∠A+∠E+∠D=360°;(2)40;(3)∠AED=![]() ∠AFC-90°.
∠AFC-90°.
【解析】
(1)根据∠B、∠C的度数和多边形内角和公式即可得出结论;
(2)过E作EM⊥BC于M.由平移的性质可知:E′在EM上,四边形AA'E'E和四边形E'CDE是平行四边形,多边形AA'E'CDE的面积=四边形AA'E'E的面积+四边形E'CDE的面积,根据平行四边形的面积计算公式代入即可得出结论;
(3)过F作FM∥AB.设∠EAF=x,∠E'CF=y,根据平行线的性质可得:x-y=90°-![]() ∠AFC.由(1)得:∠AED=180°-3(x-y),代入即可得出结论.
∠AFC.由(1)得:∠AED=180°-3(x-y),代入即可得出结论.
(1)∵五边形的内角和=(5-2)×180°=540°,∠B=∠C=90°,∴∠A+∠E+∠D=540°-90°-90°=360°;
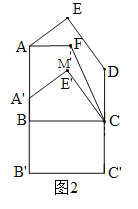
(2)作图如图1.过E作EM⊥BC于M.由平移的性质可知:E′在EM上,四边形AA'E'E和四边形E'CDE是平行四边形,∴AA'=EE'=DC=5,多边形AA'E'CDE的面积=四边形AA'E'E的面积+四边形E'CDE的面积=AA'×BM+DC×MC=DC×(BM+MC)=DC×BC=5×8=40.
(3)如图2,过F作FM∥AB.设∠EAF=x,∠E'CF=y,则∠FAB=2x,∠EAB=3x,∠FCD=2y,∠E'CD=3y.
∵FM∥AB,AB∥DC,∴∠FAB+∠AFM=180°,FM∥DC,∴∠MFC=∠FCD=2y,∴∠AFC=∠AFM+∠CFM=180°-2x+2y=180°-2(x-y),∴x-y=![]() =90°-
=90°-![]() ∠AFC.
∠AFC.
由(1)得:∠AED=360°-(∠EAB+∠EDC)=360°-(3x+180°-3y)=180°-3(x-y),∴∠AED=180°-3(90°-![]() ∠AFC)=
∠AFC)=![]() ∠AFC-90°.
∠AFC-90°.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案