题目内容
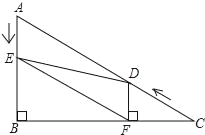
【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正确结论有( )

A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】
利用边角边即可证明△ACE与△DCB全等,然后根据全等三角形对应角相等可得∠CAM=∠CDN,再利用角边角证明△ACM≌△DCN,根据全等三角形对应边相等可得CM=CN,DN=AM,同理可证明△BCN≌△ECM,根据全等三角形对应边相等可得BN=EM,根据三角形面积公式求出CQ=CH,即可判断④,根据三角形外角性质推出∠APD=60°.
∵△DAC和△EBC都是等边三角形,
∴∠ACD=∠BCE=60°,
∴∠ACE=∠DCB=120°,
在△ACE与△DCB中,
AC=DC,∠ACE=∠DCB,CB=CE,
∴△ACE≌△DCB(SAS),故①正确;
∴∠CAM=∠CDN,
在△ACM与△DCN中
∠CAM=∠CDN,AC=DC,∠ACM=∠DCN=60°,
∴△ACM≌△DCN(ASA),
∴CM=CN,故②正确;
DN=AM,
在△AMC中,AC>AM,
∴AC≠DN,故③错误;
过C作CQ⊥DB于Q,CH⊥AE于H,
∵△ACM≌△DCN,
∴△ACM和△DCN的面积相等,
∵DN=AM,
∴由三角形面积公式得:CQ=CH,
∴CP平分∠APB,∴④正确;
∵△ACE≌△DCB,
∴∠AEC=∠DBC,
∵∠ECB=60°,
∴∠EAC+∠AEC=∠ECB=60°,
∴∠APD=∠EAC+∠ABP=∠EAC+∠AEC=60°
∴⑤正确;
故选B.

练习册系列答案
相关题目