Question

【题目】（本题满分9分）小明一直对四边形很感兴趣，在矩形ABCD中，E是AC上任意一点，连接DE，作DE⊥EF，交AB于点F．请你跟着他一起解决下列问题：

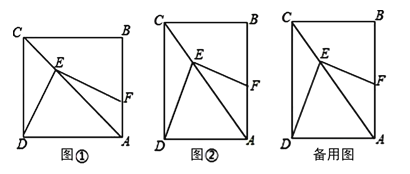
（1）如图①，若AB=BC，则DE，EF有什么数量关系？请给出证明．

（2）如图②，若∠CAB=30°，则DE，EF又有什么数量关系？请给出证明．

（3）由（1）、（2）这两种特殊情况，小明提出问题：如果在矩形ABCD中，BC=mAB，那DE，EF有什么数量关系？请给出证明．

Answer 1

【答案】（1）DE=EF．（2）DE=EF．（3）DE=EF.

【解析】试题分析：（1）根据正方形的性质得到∠EAH=45°，得到HE=HA，根据正方形的判定定理证明四边形AHEG是正方形，证明△EDG≌△EFH，得到答案；（2）根据相似三角形的性质定理解答；（3）根据相似三角形的性质定理列出比例式解答．

试题解析：（1）DE=EF．

过点E作EG⊥AD与G，EH⊥AB于H，

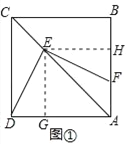
则∠EGD=∠EHF=90°，又∠BAD=90°，

∴四边形EGAH是矩形，

∵四边形ABCD是矩形，AB=AD，

∴矩形ABCD为正方形，

∴∠EAH=45°，

∴HE=HA，

∴四边形AHEG是正方形，

∴EH=EG，∠GEH=90°，

∴∠FED﹣∠GEF=∠GEH﹣∠GEF，

即∠DEG=∠FEH，

在△EDG和△EFH中，

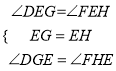
∴△EDG≌△EFH

∴DE=EF；

（2）DE=EF．

∵∠CAB=30°，

∴，

同（1）得，∠EGD=∠EHF=90°，∠DEG=∠FEH

∴△EDG∽△EFH，

∴，

∴DE=EF；

（3）DE=EF．

同（2）得，△EDG∽△EFH，

∴，

∴DE=EF．