题目内容
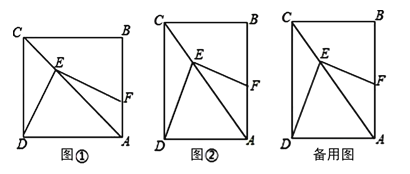
【题目】如图，抛物线y=ax2+3x+c经过A（﹣1，0），B（4，0）两点，与y轴交于点C．
（1）求抛物线的解析式；
（2）若点P在第一象限的抛物线上，且点P的横坐标为t，过点P向x轴作垂线交直线BC于点Q，设线段PQ的长为m，求m与t之间的函数关系式，并求出m的最大值；
（3）当PQ的长度取最大值时，PQ与x轴的交点记为D，在x轴上是否存在点E，使以点B，C，E为顶点的三角形与△BQD相似.如果存在，直接写出E点坐标，如果不存在，请说明理由.
【答案】（1）y=﹣x2+3x+4．（2）存在E（-4.0）或（0，0）或（4+4
，0）
【解析】试题分析：（1）将点A、B的坐标代入抛物线的解析式得到关于a、c的方程组，从而可求得a、c的值；（2）先求得点C的坐标，然后依据待定系数法求得直线BC的解析式，由直线可抛物线的解析式可知P（t，-t2+3t+4），Q（t，-t+4），从而可求得QP与t的关系式，最后依据配方法可求得m的最大值；
（3）根据条件，利用相似三角形的性质即可求解.
试题解析：（1）∵抛物线y=ax2+3x+c经过A（﹣1，0），B（4，0）两点，
∴
解得：a=﹣1，c=4．
∴抛物线的解析式为y=﹣x2+3x+4．
（2）∵将x=0代入抛物线的解析式得：y=4，
∴C（0，4）．
设直线BC的解析式为y=kx+b．
∵将B（4，0），C（0，4）代入得： 
，解得：k=﹣1，b=4
∴直线BC的解析式为：y=﹣x+4．
过点P作x的垂线PQ，如图所示：
∵点P的横坐标为t，
∴ P（t，-t2+3t+4），Q（t，-t+4）．
∴PQ=﹣t2+3t+4﹣（﹣t+4）=﹣t2+4t．
∴m=﹣t2+4t=﹣（t﹣2）2+4（0＜t＜4）．
∴当t=2时，m的最大值为4．
（3）存在E（-4.0）或（0，0）或（4+4
，0）
【题目】阅读理解：由面积都是1的小正方格组成的方格平面叫做格点平面．而纵横两组平行线的交点叫做格点．如图1中，有9个格点，如果一个正方形的每个顶点都在格点上，那么这个正方形称为格点正方形．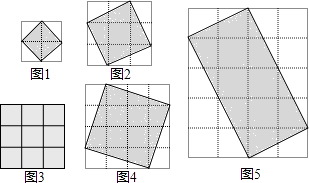 
（1）探索发现：按照图形完成下表：
格点正方形边上格点数p | 格点正方形内格点数q |
| 格点正方形面积S | |
图1 | 4 | 1 | 2 | |
图2 | 4 | 4 | ||
图3 | 4 | 9 | ||
图4 | 4 |
关于格点正方形的面积S，从上述表格中你发现了什么规律？
（2）继续猜想：类比格点正方形的概念，如果一个长方形的每个顶点都在格点上，那么这个长方形称为格点长方形，对于格点长方形的面积，你认为也有类似（1）中的规律吗？试以图5中格点长方形为例来说明．
