题目内容
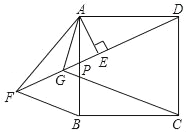
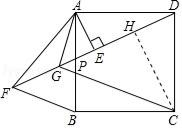
【题目】如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:△AEG是等腰直角三角形;
(2)求证:AG+CG=![]() DG.
DG.
【答案】证明见解析
【解析】试题分析:(1)根据线段垂直平分线的定义得到AF=AD,根据等腰三角形的性质、角平分线的定义证明即可;
(2)作CH⊥DP,交DP于H点,证明△ADE≌△DCH(AAS),得到CH=DE,DH=AE=EG,证明CG=![]() GH,AG=
GH,AG=![]() DH,计算即可.
DH,计算即可.
试题解析:
(1)证明:∵DE=EF,AE⊥DP,
∴AF=AD,
∴∠AFD=∠ADF,
∵∠ADF+∠DAE=∠PAE+∠DAE=90°,
∴∠AFD=∠PAE,
∵AG平分∠BAF,
∴∠FAG=∠GAP.
∵∠AFD+∠FAE=90°,
∴∠AFD+∠PAE+∠FAP=90°
∴2∠GAP+2∠PAE=90°,
即∠GAE=45°,
∴△AGE为等腰直角三角形;
(2)证明:作CH⊥DP,交DP于H点,
∴∠DHC=90°.
∵AE⊥DP,
∴∠AED=90°,
∴∠AED=∠DHC.
∵∠ADE+∠CDH=90°,∠CDH+∠DCH=90°,
∴∠ADE=∠DCH.
∵在△ADE和△DCH中,
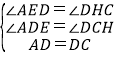 ,
,
∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=EG.
∴EH+EG=EH+HD,
即GH=ED,
∴GH=CH.
∴CG=GH.
∵AG=![]() EG,
EG,
∴AG=![]() DH,
DH,
∴CG+AG=![]() GH+
GH+![]() HD,
HD,
∴CG+AG=![]() (GH+HD),
(GH+HD),
即CG+AG=![]() DG.
DG.

练习册系列答案
相关题目