题目内容
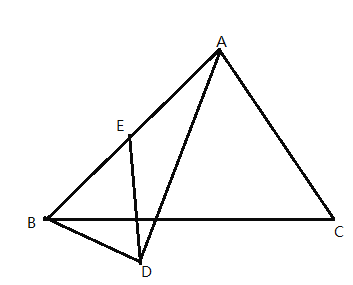
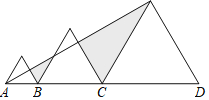
【题目】已知三个边长分别为1,2,3的正三角形从左到右如图排列,则图中阴影部分面积为______.
【答案】![]()
【解析】
将图中阴影部分的面积转换,利用等边三角形性质证明阴影部分三角形为特殊直角三角形即可解题.
如下图,设AC交BE、BF、CF与点M、N、H,
∵AB=1,BC=2,CD=3,
∴AC=CG,
∴∠CAG=∠CGA=30°,
∴AG⊥BE,
又∵∠EBA=∠FCA=60°,
∴EB∥CF,AG⊥CF,
∴AH=HG,AM=MN,(三线合一)
∴S△CHG=S△CHA,
同理, S△BMN=S△BMA,
在Rt△ABM中,AB=1,BM=![]() AB=
AB=![]() ,AM=
,AM=![]() ,
,
∴S△ABM=![]() BM
BM![]() AM=
AM=![]() =
=![]() ,
,
同理可证S△ACH=![]() CH
CH![]() AH=
AH=![]() =
=![]() ,
,
∴阴影部分面积= S△ABM+S△ACH=![]() =
=![]()

练习册系列答案
相关题目