题目内容
【题目】如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
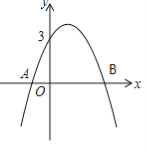
(1)求点B的坐标
(2)求该二次函数的关系式;
(3)结合图象,解答下列问题:
①当x取什么值时,该函数的图象在x轴上方?
②当-1<x<2时,求函数y的取值范围.
【答案】(1) (3,0);(2) y=-x2+2x+3; (3) ①-1<x<3; ②0<y≤4.
【解析】
试题(1)根据对称性可求出B点坐标;
(2)将A坐标代入二次函数解析式中,利用对称轴公式列出关系式,联立求出a与b的值,即可确定出二次函数解析式;
(3)①由二次函数图象与x轴的交点及对称轴求出另一个交点坐标,利用图象即可得出,该函数的图象在x轴上方时x的范围;
②根据二次函数的性质求出y的最大值,根据x的范围即可确定出y的范围.
试题解析:(1)已知点A(-1,0)及对称轴为直线x=1,知点B的坐标为(3,0);
(2)根据题意可得:
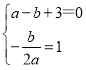 ,解得:
,解得:![]() ,
,
则二次函数解析式为y=-x2+2x+3=-(x-1)2+4;
(3)①∵函数图象与x轴的一个交点坐标为A(-1,0),且对称轴为直线x=1,
∴函数图象与x轴的另一个交点为(3,0),
∴当-1<x<3时,该函数的图象在x轴上方;
②∵函数的顶点坐标为(1,4),
∴当x=1时,y的最大值为4,
∴当-1<x<2时,函数y的取值范围为0<y≤4.
考点: 1.待定系数法求二次函数解析式;2.二次函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目