题目内容
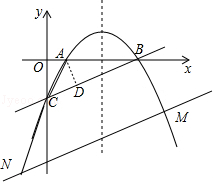
【题目】如图，抛物线y=ax2+bx﹣2经过点A（1，0）和点B（4，0），与y轴交于点C．
附：阅读材料
法国弗朗索瓦韦达最早发现一元二次方程中根与系数的关系为：两根之和等于一次项系数与二次项系数之比的相反数，两根之积等于常数项羽二次项系数之比，人们称之为韦达定理．
即：设一元二次方程ax2+bx+c=0的两根为x1、x2 ， 则：x1+x2=﹣ 
，x1x2= 
能灵活运用韦达定理，有时可以使解题更为简单．
（1）求抛物线的解析式；
（2）以点A为圆心，作于直线BC相切的⊙A，求⊙A的面积；
（3）将直线BC向下平移n个单位后与抛物线交于点M、N，且线段MN=2CB，求直线MN的解析式及平移距离．
【答案】
（1）
解：设抛物线解析式为y=a（x﹣1）（x﹣4），
即y=ax2﹣5ax+4a，
∴4a=﹣2，解得a=﹣ 
，
∴抛物线解析式为y=﹣ x2+ 
x﹣2；
（2）
解：作AD⊥BC于D，如图，当x=0时，y=﹣ x2+ x﹣2=﹣2，则C（0，﹣2），
BC= 
=2 
；
∵∠ABD=∠CBO，
∴Rt△BAD∽Rt△BCO，
∴ 
= 
，即 
= 
，
∴AD= 
，
∵直线BC相切的⊙A，
∴AD为⊙A的半径，
∴⊙A的面积=π（ ）2= 
π；
（3）
解：设直线BC的解析式为y=kx+m，
把B（4，0），C（0，﹣2）代入得 
，解得 
，
∴直线BC的解析式为y= x﹣2，
设直线MN的解析式为y= x+t，M（x1，y1），N（x2，y2），
则x1、x2为方程﹣ x2+ x﹣2= x+2t的两根，
方程整理为x2﹣4x+2t+4=0，
∴x1+x2=4，x1x2=2t+4，
∵y1﹣y2= x1+t﹣（ x2+t）= （x1﹣x2），
∴MN= 
= 
= 
= 
= 
，
∵MN=2CB，
∴ =4 ，解得t=﹣8，
∴直线MN的解析式为y= x﹣8，
∴将直线BC向下平移6个单位得到直线MN，即平移的距离为6．
【解析】（1）设交点式y=a（x﹣1）（x﹣4），即y=ax2﹣5ax+4a，然后利用4a=﹣2求出a即可得到抛物线解析式；（2）作AD⊥BC于D，如图，先确定C（0，﹣2），计算出BC=2 ，再证明Rt△BAD∽Rt△BCO，利用相似比可计算出AD= ，然后利用切线的性质得到圆的半径为AD，再利用圆的面积公式求解；（3）先利用待定系数法确定直线BC的解析式为y= x﹣2，则可设直线MN的解析式为y= x+t，M（x1 ， y1），N（x2 ， y2），利用两函数的交点问题得到x1、x2为方程﹣ x2+ x﹣2= x+2t的两根，利用根与系数的关系得x1+x2=4，x1x2=2t+4，则y1﹣y2= （x1﹣x2），接着利用两点间的距离公式和完全平方公式得到MN= = ，所以 =4 ，解方程得到t的值，从而得到直线MN的解析式，然后利用直线平移的规律确定平移的距离．
【考点精析】本题主要考查了根与系数的关系和确定一次函数的表达式的相关知识点，需要掌握一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商；确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法才能正确解答此题．
