题目内容
【题目】已知,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别是
的坐标分别是![]() ,
,![]() 且
且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)在坐标轴上是否存在点![]() ,使三角形
,使三角形![]() 的面积是8?若存在,求出点
的面积是8?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)a=-4,b=2;(2)点C的坐标是(6,0)或(-2,0)或(0,4)或(0,-12)时,三角形![]() 的面积是8.
的面积是8.
【解析】
(1)根据绝对值的非负性和绝对值的非负性即可得到答案;
(2)由(1)得到点A、B的坐标,分两种情况设点C的坐标列方程求解即可.
(1)∵![]() ,
,
∴a+4=0,b-2=0
∴a=-4,b=2;
(2)存在,理由如下:
由(1)得到A(4,4),B(2,0),
分两种情况:
①当点C在x轴上时,设点C的坐标是(x,0),
∵三角形![]() 的面积是8,
的面积是8,
∴![]() ,
,
∴![]() ,
,
解得x=6或-2,
∴C(6,0)或(-2,0);
②当点C在y轴上时,设点C的坐标是(0,y),
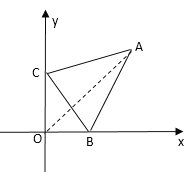
当点C在y轴正半轴上时,如图,连接OA,
∵三角形![]() 的面积是8,
的面积是8,
∴![]() ,
,
∴![]() ,
,
解得y=4,
∴点C(0,4);
当点C在y轴负半轴上时,如图,连接OA,
∵三角形![]() 的面积是8,
的面积是8,
∴![]() ,
,
∴ ![]() ,
,
∴![]() ,
,
解得y=-12或y=4(不合题意,舍去)
∴点C的坐标是(0,-12)
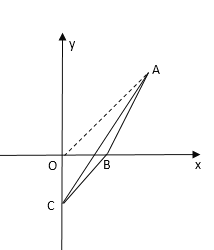
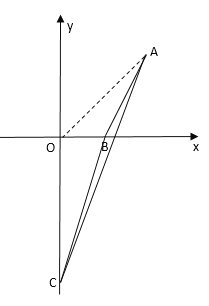
综上,点C的坐标是(6,0)或(-2,0)或(0,4)或(0,-12)时,三角形![]() 的面积是8.
的面积是8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目