题目内容
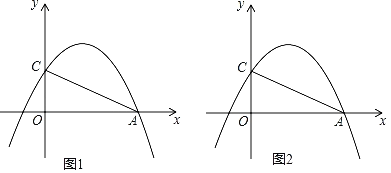
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() x2+bx+c的图象经过点A(4,0),C(0,2).
x2+bx+c的图象经过点A(4,0),C(0,2).
(1)求抛物线的表达式;
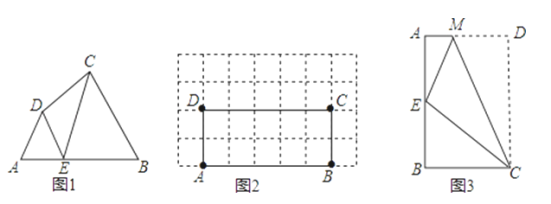
(2)如图1,点E是第一象限的抛物线上的一个动点.当△ACE面积最大时,请求出点E的坐标;
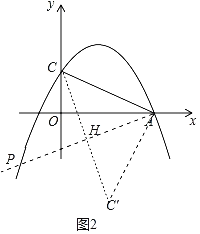
(3)如图2,在抛物线上是否存在一点P,使∠CAP=45°?若存在,求点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2.(2)当x=2时,S△ACE取得最大值4.(3)(﹣
x+2.(2)当x=2时,S△ACE取得最大值4.(3)(﹣![]() ,﹣
,﹣![]() )
)
【解析】
(1)由题意可得点A(4,0),C(0,2),用待定系数法求解即可得到答案.(2)过点E作EF∥y轴交AC于点F,用待定系数法得到直线AC的解析式为y=﹣![]() x+2,设点E(x,﹣
x+2,设点E(x,﹣![]() x2+
x2+![]() x+2),则F(x,﹣
x+2),则F(x,﹣![]() x+2),则EF=﹣
x+2),则EF=﹣![]() x2+
x2+![]() x+2﹣(﹣
x+2﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x2+2x,所以由S△ACE=S△CEF+S△AEF得到二次函数,根据二次函数的顶点即可解答.(3)如图2中,将线段AC绕点A逆时针旋转90°得到AC′,则C′(2,4),取CC′的中点H(1,1),作直线AH交抛物线于P,此时∠PAC=45°,求出直线AH的解析式,构建方程组即可解决问题.
x2+2x,所以由S△ACE=S△CEF+S△AEF得到二次函数,根据二次函数的顶点即可解答.(3)如图2中,将线段AC绕点A逆时针旋转90°得到AC′,则C′(2,4),取CC′的中点H(1,1),作直线AH交抛物线于P,此时∠PAC=45°,求出直线AH的解析式,构建方程组即可解决问题.
解:(1)将点A(4,0),C(0,2)代入y=﹣![]() x2+bx+c得:
x2+bx+c得:
![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+2.
x+2.
(2)如图1,过点E作EF∥y轴交AC于点F,
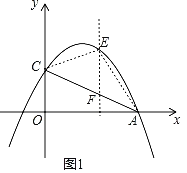
设直线AC的解析式为y=kx
∴4k+2=0,
∴k=﹣![]() ,
,
∴直线AC的解析式为y=﹣![]() x+2,
x+2,
设点E(x,﹣![]() x2+
x2+![]() x+2),则F(x,﹣
x+2),则F(x,﹣![]() x+2),
x+2),
则EF=﹣![]() x2+
x2+![]() x+2﹣(﹣
x+2﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x2+2x,
x2+2x,
∴S△ACE=S△CEF+S△AEF=![]() EFOA=
EFOA=![]() (﹣
(﹣![]() x2+2x)×4=﹣x2+4x=﹣(x﹣2)2+4,
x2+2x)×4=﹣x2+4x=﹣(x﹣2)2+4,
∵﹣1<0,
∴当x=2时,S△ACE取得最大值4.
(3)如图2中,将线段AC绕点A逆时针旋转90°得到AC′,则C′(2,﹣4),取CC′的中点H(1,﹣1),作直线AH交抛物线于P,此时∠PAC=45°,
∵A(4,0),H(1,﹣1),
∴直线AH的解析式为y=![]() x﹣
x﹣![]() ,
,
由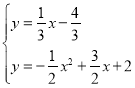 ,解得
,解得![]() 或
或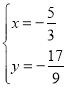 ,
,
∴P(![]() ,
, ![]() ).
).
作直线AP′⊥PA,则直线AP′的解析式为y=﹣3x+12,
由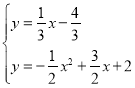 ,解得
,解得![]() 或
或![]() (不合题意舍弃),
(不合题意舍弃),
综上所述,满足条件的点P的坐标为(﹣![]() ,﹣
,﹣![]() )
)

 全能测控一本好卷系列答案
全能测控一本好卷系列答案