题目内容
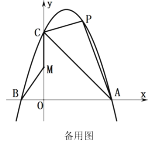
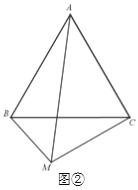
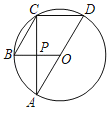
【题目】如图,AD是⊙O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,给出下列结论:①AC⊥CD;②∠CAD=30°;③OB⊥AC;④CD=2OP.其中正确的个数为( )
A.4个B.3个C.2个D.1个
【答案】A
【解析】
利用直径所对的圆周角是直角判断①,利用四边形OBCD是平行四边形证明![]() 是等边三角形,可判断②,利用平行四边形与结论①,可判断③,利用中位线的性质可判断④.
是等边三角形,可判断②,利用平行四边形与结论①,可判断③,利用中位线的性质可判断④.
∵AD是⊙O的直径,
∴∠ACD=90°,
∴AC⊥CD,故①正确;
如图,连接OC,
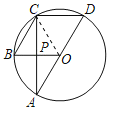
∵四边形OBCD是平行四边形,
∴BC=OD,OB=CD
∵OB=OC=OD,
∴OB=OC=BC=OD=CD,
∴△BOC与△COD均为等边三角形,
∴∠COD=60°,∠BOC=60°,
∴∠CAD=![]() ∠COB=30°,故②正确;
∠COB=30°,故②正确;
∵四边形OBCD是平行四边形,
∴OB∥CD,
∵AC⊥CD,
∴OB⊥AC,故③正确;
∵OB⊥AC,
∴CP=AP,
又∵OA=OD,
∴CD=2OP,故④正确.
综上,正确的有①②③④.
故选:A.

练习册系列答案
相关题目