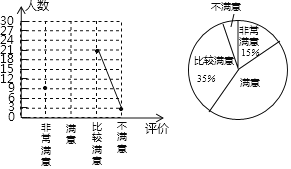
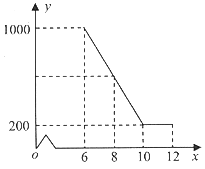
题目内容
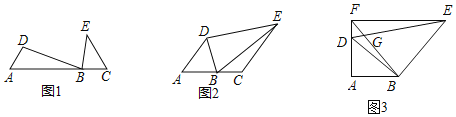
【题目】如图,∠A=∠DBE=α,
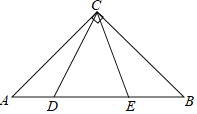
(1)如图1,若C点在射线AB上,且∠C=α,求证:![]() ;
;
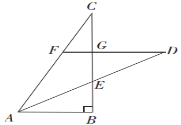
(2)如图2,若C在射线AB上,α=60°,∠ABD=75°,EC∥AD,EC=2AB=4,求S四边形BCED;
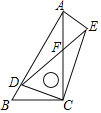
(3)如图3,若α=90°,BD平分∠ADE,EF⊥AD于F,线段BF、DE交于G,若![]() ,直接写出
,直接写出![]() 的值(用含m,n的式子表示).
的值(用含m,n的式子表示).
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)如图1,证明△DAB∽△BCE,可解答;
(2)如图2,作辅助线,构建30°的直角三角形和等腰直角三角形,分别计算BE、DH、BC和EF的长,根据S四边形BCED=S△BDE+S△BCE可解答;
(3)如图3,作辅助线,构建相似三角形,证明△EFD∽△HAD和△EFG∽△HBG,列比例式可解答.
(1)证明:如图1,

∵∠A=∠DBE=α,
∴∠D+∠ABD=∠ABD+∠EBC=180°-α,
∴∠D=∠EBC,
∵∠A=∠C=α,
∴△DAB∽△BCE,
∴![]() ;
;
(2)解:如图2,过B作BG⊥AD于G,过D作DH⊥BE于H,过E作EF⊥AC于F,

∵∠DAB=60°,∠ABD=75°,
∴∠ADB=180°-60°-75°=45°,
Rt△ABG中,∠ABG=30°,AB=2,
∴AG=1,BG=![]() ,
,
∵△BDG是等腰直角三角形,
∴BD=![]() BG=
BG=![]() ,
,
∵∠DBE=α=60°,
Rt△DBH中,∠BDH=30°,
∴![]() ,
,
∵∠ABD=75°,∠DBE=60°,
∴∠EBF=45°,
∴△EBF是等腰直角三角形,
∵EC∥AD,
∴∠ECF=∠A=60°,
Rt△ECF中,∠CEF=30°,
∵EC=4,
∴CF=2,EF=BF=2![]() ,
,
∴BE=![]() EF=2
EF=2![]() ;
;
∴S四边形BCED=S△BDE+S△BCE
=![]() ;
;
(3)解:如图3,过B作BM⊥DE于M,过E作EC⊥AB于C,延长ED、BA交于H,
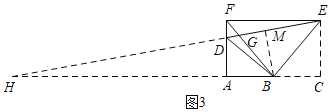
∵BD平分∠ADE,∠DAB=90°,
∴AB=BM,
∵∠DBE=α=90°,
∴∠CBE+∠ABD=∠ABD+∠ADB=90°,
∴∠CBE=∠ADB=∠BDE,
∵∠DBE=∠C=90°,
∴∠DEB=∠CEB,
∴BM=BC,
∴BC=AB,
∵EF⊥AD,
∴∠EFA=90°,
∵∠FAC=∠C=90°,
∴四边形FACE是矩形,
∴EF=AC,
设AB=x,则EF=2x,
∵EF∥CH,
∴△EFD∽△HAD,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵EF∥BH,
∴△EFG∽△HBG,
∴ .
.

 名校课堂系列答案
名校课堂系列答案