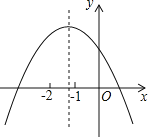题目内容
【题目】以下四个命题:![]() 用换元法解分式方程
用换元法解分式方程![]() 时,如果设
时,如果设![]() ,那么可以将原方程化为关于
,那么可以将原方程化为关于![]() 的整式方程
的整式方程![]() ;
;![]() 如果半径
如果半径![]() 为的圆的内接正五边形的边长为
为的圆的内接正五边形的边长为![]() ,那么
,那么![]() ;
;![]() 有一个圆锥,与底面圆直径是
有一个圆锥,与底面圆直径是![]() 且体积为
且体积为![]() 的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为
的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为![]() ;④二次函数
;④二次函数![]() ,自变量的两个值
,自变量的两个值![]() 对应的函数值分别为
对应的函数值分别为![]() ,若
,若![]() ,则
,则![]() .其中正确的命题的个数为( )
.其中正确的命题的个数为( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
【答案】D
【解析】
①利用换元法代入并化简;
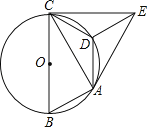
②作OF⊥BC,在Rt△OCF中,利用三角函数求出a的长;
③这个圆锥母线长为R,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到![]() ,然后解关于R的方程即可;
,然后解关于R的方程即可;
④根据二次函数图象的性质和绝对值的意义进行判断可得出正确的结论.
解:![]() 设
设![]() ,那么可以将原方程化为关于
,那么可以将原方程化为关于![]() 的整式方程
的整式方程![]() ,故正确;
,故正确;
![]() 作
作![]() .
.

∵∠COF=72°÷2=36°,
∴CF=rsin36°,
∴CB=2rsin36°,即a=2rsin36°=2rcos54°.
故正确;
③设圆锥的高为h,底面半径为r,母线长为R,
根据题意得![]() ,
,
则R:r=2:1.
由 得到
得到![]()
所以h2+r2=R2,即 ,则
,则![]()
即它的母线长是![]()
故正确;
④二次函数y=ax2-2ax+1的对称轴是x=1,所以![]() 表示自变量为x时,对应点离对称轴的距离。
表示自变量为x时,对应点离对称轴的距离。
当a<0时图象开口向下,由下图可知对应点离对称轴越远所对应的函数值越小。
∵![]()
∴y1<y2
所以a(y1-y2)>0.
当a>0时图象开口向上,对应点离对称轴越远所对应的函数值越大。
∵![]()
∴y1>y2
所以a(y1-y2)>0.
故本命题正确.
综上所述,正确的命题的个数为4个.
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目