题目内容
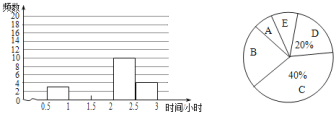
【题目】某校为了解本校学生对课后服务情况的评价，随机抽取了部分学生进行调查，根据调查结果制成了如下不完整的统计图．
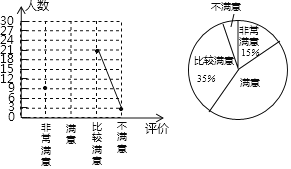
根据统计图：
（1）求该校被调查的学生总数及评价为“满意”的人数；
（2）补全折线统计图；
（3）根据调查结果，若要在全校学生中随机抽1名学生，估计该学生的评价为“非常满意”或“满意”的概率是多少？
【答案】（1）27人；（2）见解析；（3）
【解析】
（1）首先求得总人数，然后根据百分比求得人数即可；
（2）根据（1）补全折线统计图即可；
（3）利用概率公式求解即可．
解：（1）由折线统计图知“非常满意”9人，由扇形统计图知“非常满意”占15%，所以被调查学生总数为
（人），所以“满意”的人数为
（人）；
（2）如图：
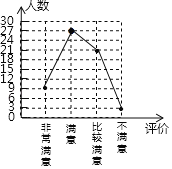
（3）所求概率为
．
练习册系列答案
相关题目
【题目】襄阳市某农谷生态园响应国家发展有机农业政策，大力种植有机蔬菜．某超市看好甲、乙两种有机蔬菜的市场价值，经调查，这两种蔬菜的进价和售价如下表所示：
有机蔬菜种类 | 进价（元/ | 售价（元/ |
甲 |
| 16 |
乙 |
| 18 |
（1）该超市购进甲种蔬菜10
和乙种蔬菜5需要170元；购进甲种蔬菜6和乙种蔬菜10需要200元．求
，
的值；
（2）该超市决定每天购进甲、乙两种蔬菜共100进行销售，其中甲种蔬菜的数量不少于20，且不大于70．实际销售时，由于多种因素的影响，甲种蔬菜超过60的部分，当天需要打5折才能售完，乙种蔬菜能按售价卖完．求超市当天售完这两种蔬菜获得的利润额
（元）与购进甲种蔬菜的数量
（）之间的函数关系式，并写出的取值范围；
（3）在（2）的条件下，超市在获得的利润额（元）取得最大值时，决定售出的甲种蔬菜每千克捐出
元，乙种蔬菜每千克捐出
元给当地福利院，若要保证捐款后的盈利率不低于20%，求的最大值．
