题目内容
【题目】四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)
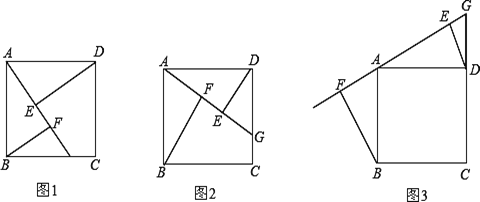
如图1,点G是BC边上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E.求证:△ABF≌△DAE;
(2) ①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E,线段EF与AF、BF的等量关系是______ ___;
②如图3,若点G是CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,
线段EF与AF、BF的等量关系是______ ;
(3)若点G是BC延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,请画图并
探究线段EF与AF、BF的等量关系.
【答案】(1)详见解析;(2)① EF=BF-AF;②EF=AF+BF;(3)详见解析.
【解析】试题分析:(1) 利用正方形边相等和直角三角形角互余,证明△ABF和△DAE全等.
(2)画图,方法同(1)
(3)利用正方形的边的性质,证明△ABF和△DAE全等,
试题解析:
证明:(1)∵BF⊥AG,DE⊥AG
∴∠AFB=∠DEA=90°,
∵∠BAD=90°,
∴∠BAF=∠ADE(同角的余角相等),
∵四边形ABCD是正方形,
∴AB=AD,
在△ABF和△DAE中,
 ,
,
∴△ABF≌△DAE(AAS).
(2)①故答案为: EF=BF-AF,
② 故答案为:EF=AF+BF,
(3)如图4,
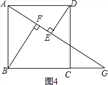
∵BF⊥AG,DE⊥AG,
∴∠AFB=∠DEA=90°,
∵∠BAD=90°,
∴∠BAF=∠ADE(同角的余角相等)
∵四边形ABCD是正方形,
∴AB=AD,
在△ABF和△DAE中
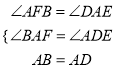 ,
,
∴△ABF≌△DAE(AAS),
∴AE=BF,
∴EF=AE-AF=BF-AF,
即EF=BF-AF.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案