题目内容
【题目】已知如图,直线AB、CD相交于点O,∠COE=90°. 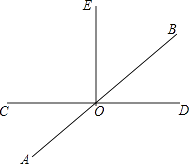
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
【答案】
(1)解:∵∠AOC=36°,∠COE=90°,
∴∠BOE=180°﹣∠AOC﹣∠COE=54°
(2)解:∵∠BOD:∠BOC=1:5,
∴∠BOD=180°× ![]() =30°,
=30°,
∴∠AOC=30°,
∴∠AOE=30°+90°=120°
(3)解:如图1,∠EOF=120°﹣90°=30°,
或如图2,∠EOF=360°﹣120°﹣90°=150°.
故∠EOF的度数是30°或150°.

【解析】(1)根据平角的定义求解即可;(2)根据平角的定义可求∠BOD,根据对顶角的定义可求∠AOC,根据角的和差关系可求∠AOE的度数;(3)先过点O作OF⊥AB,再分两种情况根据角的和差关系可求∠EOF的度数.
【考点精析】本题主要考查了对顶角和邻补角的相关知识点,需要掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目