题目内容
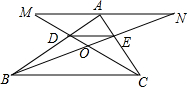如图在△ABC中，D，E分别在边AB，AC上，且DE∥BC，过点A作平行于BC的直线分别交CD和BE的延长线于点M，N，若DE=2，BC=6，．（1）求BO：OE：EN；
（2）求MN的长．
分析：（1）根据平行线分线段成比例定理求出
，
，然后求出
，整理即可得解；
（2）利用平行线分线段成比例定理列式整理即可得解．
| OE |
| BO |
| AE |
| AC |
| OE |
| EN |
（2）利用平行线分线段成比例定理列式整理即可得解．
解答：解：（1）∵DE∥BC，
∴
=
=
=
=
，
∵MN∥BC，
∴
=
=
，
∴
=
，
设EN=k，则BE=2k，
∴OE=
×2k=
，
∴
=
=
，
∴BO：OE：EN=3：1：2；
（2）∵MN∥BC，
∴
=
，
∴
=
，
∴MN=6．
∴
| OE |
| BO |
| AE |
| AC |
| DE |
| BC |
| 2 |
| 6 |
| 1 |
| 3 |
∵MN∥BC，
∴
| EN |
| BN |
| AE |
| AC |
| 1 |
| 3 |
∴
| EN |
| BE |
| 1 |
| 2 |
设EN=k，则BE=2k，
∴OE=
| 1 |
| 3+1 |
| k |
| 2 |
∴
| OE |
| EN |
| ||
| k |
| 1 |
| 2 |
∴BO：OE：EN=3：1：2；
（2）∵MN∥BC，
∴
| BC |
| MN |
| BO |
| ON |
∴
| 6 |
| MN |
| 3 |
| 1+2 |
∴MN=6．
点评：本题考查了平行线分线段成比例定理，熟练掌握定理并准确识图是解题的关键．
练习册系列答案
相关题目
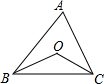如图在△ABC中，∠ABC=50°，∠ACB=75°，点O是内心，则∠BOC的度数为
如图在△ABC中，∠A=45°，tanB=3，BC=
已知，如图在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG平分∠CDE，DC=AE，
如图在△ABC中，AD垂直平分BC，AD=8，BC=10，E、F是AD上的两点，则图中阴影部分的面积是