Question

【题目】如图，在等腰直角三角形ABC中，∠C=90°，点D为AB的中点，已知扇形EAD和扇形FBD的圆心分别为点A、点B，且AB=4，则图中阴影部分的面积为_____（结果保留π）．

Answer 1

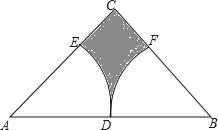
【答案】4﹣π

【解析】

由在等腰直角三角形ABC中，∠C=90°，AB=4，可求得直角边AC与BC的长，继而求得△ABC的面积，又由扇形的面积公式求得扇形EAD和扇形FBD的面积，继而求得答案．

解：∵在等腰直角三角形ABC中，∠C=90°，AB=4，

∴AC=BC=ABsin45°=AB=2，

∴S△ABC=ACBC=4，

∵点D为AB的中点，

∴AD=BD=AB=2，

∴S扇形EAD=S扇形FBD=×π×22=π，

∴S阴影=S△ABC﹣S扇形EAD﹣S扇形FBD=4﹣π．

故答案为：4﹣π．