Question

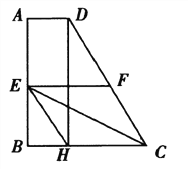
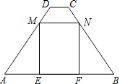
【题目】如图，在梯形ABCD中，∠A=∠B=90°，AB=，点E在AB上，∠AED=45°，DE=6，CE=7.

（1）求AE的长；

（2）求sin∠BCE的值．

Answer 1

【答案】（1）3;（2）．

【解析】

（1）在Rt△DAE中，∠A=90°，∠AED=45°，DE=6，根据这些条件利用余弦函数求AE；
（2）在Rt△BCE中，EC=7，再利用（1）的解答结果，根据正弦函数来解答sin∠BCE的值．

解：（1）在Rt△DAE中，∠A=90°，∠AED=45°，DE=6．
∵cos∠AED= ，
∴AE=DE×cos∠AED,
=6×cos45°,
=3 ．

（2）∵BE=AB-AE，
∴BE=5-3=2．

在Rt△BCE中，EC=7，
sin∠BCE== ．