Question

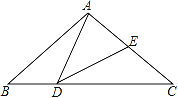
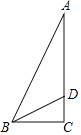
【题目】如图，△ABC中，∠C＝90°，点D为AC上一点，∠ABD＝2∠BAC＝45°，若AD＝12，则△ABD的面积为____．

Answer 1

【答案】36．

【解析】

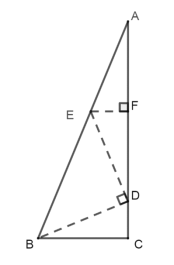
作DE⊥DB交AB于E，EF垂直AC于F，则∠DEB=90°-∠ABD=45°，证出AE=DE=DB，通过证明△AEF≌△BCD，得出BC==AF=AD=6，由三角形面积公式即可得出答案．

作DE⊥DB交AB于E，EF垂直AC于F，如图所示：

则∠DEB=90°-∠ABD=45°，

∴△BDE是等腰直角三角形，

∴DB=DE，

∵∠ABD=2∠BAC=45°，

∴∠BAC=22.5°，

∴∠ADE=∠DEB-∠BAC=22.5°=∠BAC，

∴AE=DE=DB，

∵∠AFE=90°，

∴F是AD中点，AF=FD，

又∵∠C=90°，

∴∠CBD=90°-45°-22.5°=22.5°，

在Rt△AEF和Rt△BCD中

∴Rt△AEF≌Rt△BCD（AAS），

∴AF=BC=AD=6，

∴△ABD的面积S=AD×BC=×12×6=36；

故答案为：36．