Question

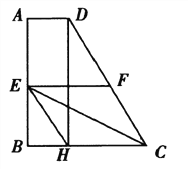
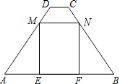
【题目】如图1，DC∥AB，∠D=90°，AC⊥BC，AB=10cm，BC=6cm. 点P以1cm/s的速度从点A出发，沿AB方向向点B运动，同时点Q以2cm/s的速度从点B出发，沿B→C→A方向向点A运动，当一个运动点到达终点时，另一个运动点也随之停止运动，设运动的时间为t(s).

（1）① 求证：△ACD∽△BAC；② 求DC的长；

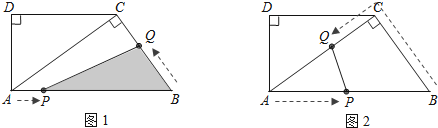
（2）当点Q在边BC上运动，求t为何值时，△PBQ的面积为cm2；

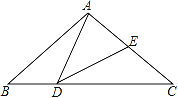
（3）如图2，当点Q在边CA上运动，求t为何值时，PQ∥BC.

Answer 1

【答案】（1）① 见解析；② DC=6.4(cm)；（2）当点Q在边BC上运动，t=2s时，△PBQ的面积为cm2；（3）当点Q在边CA上运动，t=5s时，PQ∥BC.

【解析】

（1）①根据DC∥AB，得到∠ACD=∠BAC，由于∠D=90°，AC⊥BC，于是得到∠D=∠ACB=90°，就可得到△ACD∽△BAC；
②在Rt△ABC中，由勾股定理得AC==8（cm），根据△ACD∽△BAC，列比例式即可得到结果；（2）如图1，点Q在边BC上运动，此时，0＜t≤3，过点Q作QE⊥AB于E，根据三角函数sinB=，即 ，求得QE=t，根据三角形的面积列方程即可得到结论；（3）如图2，当点Q在边CA上运动，时，PQ∥BC，列比例式得方程解得结果．

（1）①∵ DC∥AB，

∴ ∠ACD=∠BAC．

又∵ ∠D=90°，AC⊥BC，

∴ ∠D=∠ACB=90°，

∴ △ACD∽△BAC．

② 在Rt△ABC中，由勾股定理，得

AC==8(cm).

∵ △ACD∽△BAC，

∴ ，

即 ．

解得DC=6.4(cm).

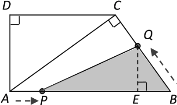
（2）如图，点Q在边BC上运动，此时，0＜t≤3.

过点Q作QE⊥AB于E，

∴ sinB=，即 ．

解得 QE=t.

∴ BP·QE=(10-t)·t=.

整理，得 t2-10t+16=0.

解这个方程，得t1=2，t2=8 (不合题意，舍去).

∴当点Q在边BC上运动，t=2s时，△PBQ的面积为cm2.

（3）如图，

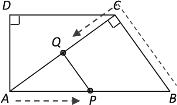
当点Q在边CA上运动，时，PQ∥BC.

∴ 即 ，解得 t=5.

∴ 当点Q在边CA上运动，t=5s时，PQ∥BC