题目内容
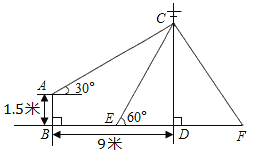
【题目】如图，电力公司在电线杆上的C处引两条等长的拉线CE、CF固定电线杆CD，拉线CE和地面成60°角，在离电线杆9米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米．
（1）求CD的长（结果保留根号）；
（2）求EF的长（结果保留根号）．
【答案】（1）
（2）
【解析】试题分析：（1）过点A作AH⊥CD，垂足为H，根据矩形的性质和直角三角形的性质可求解；
（2）在上面基础上，先证得△CEF是等边三角形，然后再根据直角三角形的性质求解.
试题解析：（1）过点A作AH⊥CD，垂足为H，
由题意可知四边形ABDH为矩形，∠CAH=30°，
∴AB=DH=1.5，BD=AH=9，
在Rt△ACH中，tan∠CAH=
，
∴CH=AH tan∠CAH，
∴CH=AH·tan∠CAH=9tan30°=9×
（米），
∵DH=1.5，
∴CD的长=（米）
（2）在Rt△CDE中，
∵∠CED=60°，sin∠CED=
，
∴CE=
=6+
米，
∴EF=CE=（米）
练习册系列答案
相关题目
【题目】在对第一章“丰富的图形世界”复习前，老师让学生整理正方体截面的形状并探究多面体（由若干个多边形所围成的几何体）的棱数、面数、顶点数之间的数量关系，如图是小颖用平面截正方体后剩余的多面体，请解答下列问题：
（1）根据上图完成下表：
多面体 | V（顶点数） | F（面数） | E（棱数） |
（1） |
| 7 | 15 |
（3） | 6 |
| 9 |
（5） | 8 | 6 |
|
（2）猜想：一个多面体的V（顶点数），F（面数），E（棱数）之间的数量关系是 ；
（3）计算：已知一个多面体有20个面、30条棱，那么这个多面体有 个顶点．
