��Ŀ����
����Ŀ����ͼ�٣�ֱ��L��y=mx+n(m<0��n>0)��x��y��ֱ��ཻ��A��B���㣬����AOB�Ƶ�O��ʱ����ת90�����õ���COD������A��B��D��������P����L�Ĺ��������ߣ���L����P�Ĺ���ֱ�ߣ�
(1)��L��y=-x+2����P��ʾ�ĺ�������ʽΪ______����P��![]() ����
����![]() ��ʾ�ĺ�������ʽΪ_______��
��ʾ�ĺ�������ʽΪ_______��
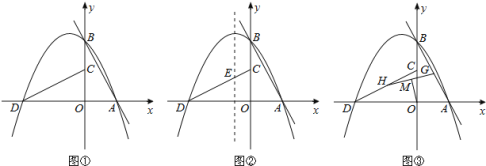
(2)��ͼ�ڣ���L��y=-3x+3��P�ĶԳ�����CD�ཻ�ڵ�E����F��L�ϣ���Q��P�ĶԳ����ϣ����Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı���ʱ�����Q�����ꣻ
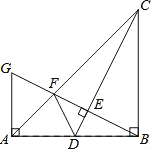
(3)��ͼ�ۣ���L��y=mx+1��GΪAB�е㣬HΪCD�е㣬����GH��MΪGH�е㣬����OM����OM=![]() �����L��P��ʾ�ĺ�������ʽ��
�����L��P��ʾ�ĺ�������ʽ��
���𰸡�(1)![]() ��y=��2x+4��(2)Q����ΪQ1(��1��
��y=��2x+4��(2)Q����ΪQ1(��1��![]() )��Q2(��1��
)��Q2(��1��![]() )��(3)y=��3x+1��y=��3x2��2x+1��
)��(3)y=��3x+1��y=��3x2��2x+1��
��������
��1����l��y=-x+2�������A��B��D�����꣬���ô���ϵ�������P��ʾ�ĺ�������ʽ����P��![]() �������D��A��B�����꣬�����ô���ϵ�������l��ʾ�ĺ�������ʽ��
�������D��A��B�����꣬�����ô���ϵ�������l��ʾ�ĺ�������ʽ��
��2�����ݶԳ���Ķ����ɣ�
��3���Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı���ʱ������FQ��CE����FQ=CE���Դ�Ϊ�������з��������Q�����꣮ע�⣺��Q�����������������ͼ��ʾ����Ҫ©�⣻
��4�����ͼ��ʾ���������ߣ��������ֱ��������OGH�����OG�ij��ȣ�������AB=2OG���AB�ij��ȣ������ù��ɶ������y=mx+1��m��ֵ�����ֱ����l��P��ʾ�ĺ�������ʽ��
�⣺(1)![]() ��y=��2x+4��
��y=��2x+4��
(2)��![]() ��y=��3x+3����A(1��0)��B(0��3)��
��y=��3x+3����A(1��0)��B(0��3)��
��C(0��1)��D(��3��0)�����ֱ��CD�Ľ���ʽΪ��y=![]() x+1�������
x+1�������![]() �ĶԳ���Ϊx=��1��
�ĶԳ���Ϊx=��1��
���Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı��Σ�
��FQ��CE����FQ=CE��
��ֱ��FQ�Ľ���ʽΪ��y=![]() x+b���ߵ�E����C�ĺ��������1��
x+b���ߵ�E����C�ĺ��������1��
���F����Q�ĺ�����Ҳ�����1����|xF��(��1)|=|xF+1|=1�����xF=0��xF=��2��
�ߵ�F��ֱ��![]() ��y=��2x+4�ϣ�
��y=��2x+4�ϣ�
���F����Ϊ(0��3)��(��2��9)��
��F(0��3)����ֱ��FQΪ��y=![]() x+3��
x+3��
��x=��1ʱ��y=![]() ����Q1(��1��
����Q1(��1��![]() ).
).
��F(��2��9)����ֱ��FQΪ��![]() ��
��
��x=��1ʱ��y= ![]() ����Q2(��1��
����Q2(��1��![]() )��
)��
�����������ĵ�Q��2�������ͼ1��ʾ����Q����ΪQ1(��1��![]() )��Q2(��1��
)��Q2(��1��![]() )��
)��
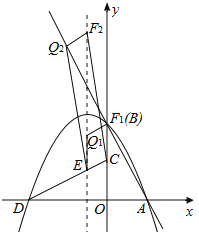
(3)��ͼ2��ʾ������OG��OH���ߵ�G��HΪб���е㣬
��OG=![]() AB��OH=
AB��OH=![]() CD��
CD��
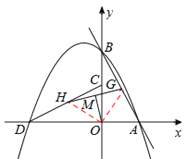
����ת���ʿ�֪��AB=CD��OG��OH��
���OGHΪ����ֱ�������Σ�
�ߵ�GΪGH�е㣬
����OMGΪ����ֱ��������.
��OG=![]() OM=
OM=![]()
![]() =
=![]() .
.
��AB=2OG=![]() ��
��
��![]() ��y=mx+1��
��y=mx+1��
��A(![]() ��0)��B(0��1)��
��0)��B(0��1)��
��Rt��AOB�У��ɹ��ɶ����ã�OA2+OB2=AB2������(![]() )2+12=(
)2+12=(![]() )2��
)2��
��ã�m=��3��m=3.
�ߵ�B��y�������ᣬ
��m=3��ȥ��
��m=��3��
��![]() ��ʾ�ĺ�������ʽΪ��y=��3x+1��
��ʾ�ĺ�������ʽΪ��y=��3x+1��
��B(0��1)��D(��1��0)����A(![]() ��0)��
��0)��
���ô���ϵ�������![]() ��y=��3x2��2x+1��
��y=��3x2��2x+1��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�