题目内容
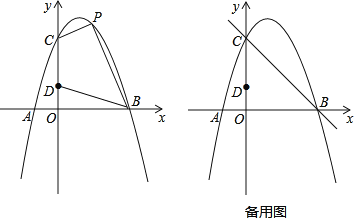
【题目】如图,抛物线y=(x+m)2+m与直线y=x相交于E,C两点(点E在点C的左边),抛物线与x轴交
于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.
⑴ 若抛物线与y轴交点坐标为(0,2),求m的值;
⑵ 求证:⊙H与直线y=1相切;
⑶ 若DE=2EC,求⊙H的半径.

【答案】(1)-2;(2)见解析;(3)3.
【解析】
(1)由抛物线y=(x+m)2+m与y轴的交点坐标为(0,2),可得m2+m=2,又由抛物线与x轴有两个交点,即可得(x+m)2+m=0有两个不相等的实数根,继而求得答案;
(2)首先作直径CM交弦AB于点G,连接HB,由抛物线y=(x+m)2+m,与直线y=-x相交于E,C两点(点E在点C的左边),可得(x+m)2+m=-x,继而可证得点C是抛物线的顶点,由抛物线与圆的对称性得:CM垂直平分AB,可证得CM⊥直线y=1,然后设A,B两点的横坐标分别为x1,x2,则x1,x2是(x+m)2+m=x2+2mx+m2+m=0的两根,可得x1+x2=-2m,x1x2=m2+m,再设⊙H的半径为r,CG=-m,HG=-m-r,易证得点H到直线y=1的距离为:-m-r+1=2r-r=r,即可得⊙H与直线y=1相切;
(3)首先连接MD,由⊙H与直线y=1相切于点M,可得△CMN是等腰直角三角形,CM为直径,易得DN=DC,则可求得EC的长,继而求得答案.
⑴ ∵抛物线y=(x+m)2+m与y轴的交点坐标为(0,2),
∴当x=0时,y=m2+m=2,解之,得,m1=-2,m2=1.
∵抛物线y=(x+m)2+m与x轴有两个交点,
∴方程x2+2mx+m2+m=0有不等的实数根,(2m)2-4(m2+m)>0,
∴m<0,∴m=-2.
⑵ 证明:作直径CM交弦AB于点G,连接HB.
由抛物线y=(x+m)2+m与直线y=-x相交于点E,C两点,
可得(x+m)2+m=-x,
∴(x+m)2+m+x=0,(x+m)(x+m+1)=0.
∴x1=-m,x2=-m-1.
因为点E在点C的左边,
所以E,C两点的坐标为E(-m-1,m+1),C(-m,m).
故点C是抛物线的顶点.由抛物线和圆的对称性知,CM垂直平分AB.
∴CM⊥直线y=1,
设A、B两点的横坐标分别为x1,x2,则x1,x2是方程x2+2mx+m2+m=0的两根.
∴x1+x2=-2m,x1x2=m2+m.
∴AB=x2-x1=![]() =2
=2![]() .
.
设⊙H的半径为r,CG=-m,HG=m-r.在Rt△HGB中,HG=-m-r,HB=r,GB=![]() .
.
∴(-m-r)2+(![]() )2=r2.r =
)2=r2.r =![]() .
.
因为HG=-m-r,
所以点H到直线y=1的距离为-m-r
所以,⊙H与直线y=1相切.
⑶ 连接MD,⊙H与直线y=1相切于点M,所以△CMN为等腰直角三角形,
∵CM为直径,
∴∠CDM=90°,
∴DN=DC.由E(-m-1,m+1),C(-m,m)可得,EC=![]() .
.
又∵DE=2EC,
∴CD=3CE=3![]() ,
,
∴CN=2CD=6![]() ,
,
∴CM=2r =6,
∴r =3.

 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案