题目内容
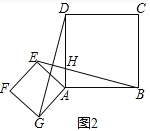
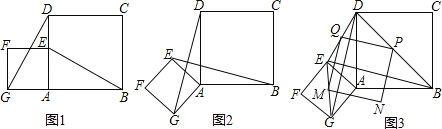
【题目】如图1所示，四边形AEFG与四边形ABCD是正方形，其中G、A、B三点在同一直线上．连接DG、BE．完成下面问题：
（1）求证：BE=DG；
（2）如图2，将正方形AEFG绕点A逆时针转过一定角度时，小明发现：BE=DG且BE⊥DG，请你帮助小明证明这两个结论；
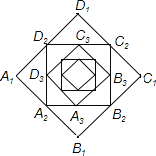
（3）如图3，小明还发现：在旋转过程中，分别连接EG、GB、BD、DE的中点，得到的四边形MNPQ是正方形．若AB=a，AE=b其中a＞b，你能帮小明求出正方形MNPQ的面积的范围吗？写出过程．
【答案】（1）见解析；（2）见解析；（3）
（a﹣b）2≤正方形MNPQ的面积≤（a+b）2．
【解析】
试题分析：（1）根据正方形的性质得到AD=AB，AE=AG，∠DAG=∠BAE=90°，证明△DAG≌△BAE，根据全等三角形的性质证明结论；
（2）根据全等三角形的性质和互余的概念以及垂直的定义证明即可；
（3）根据三角形中位线定理得到MN=
BE，根据旋转的性质和正方形的面积公式计算即可．
（1）证明：∵四边形AEFG与四边形ABCD是正方形，
∴AD=AB，AE=AG，∠DAG=∠BAE=90°，
在△DAG和△BAE中，
，
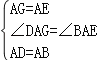∴△DAG≌△BAE，
∴BE=DG；
（2）证明：如图2，∵∠EAG=∠BAD=90°，
∴∠DAG=∠BAE，
在△DAG和△BAE中，
，
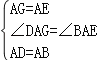∴△DAG≌△BAE，
∴BE=DG，∠ADG=∠ABE，
∵∠ABE+∠AHB=90°，∠AHB=∠DHE，
∴∠ADG+∠DHE=90°，
∴BE⊥DG，
∴BE=DG且BE⊥DG；
（3）解：∵M、N分别是EG、GB的中点，
∴MN=BE，
∴当BE最小时，正方形MNPQ是面积最小，BE最大时，正方形MNPQ是面积最大，
由题意可知，当点E旋转到线段AB上时，BE最小为a﹣b，
当点E旋转到线段AB的延长线上时，BE最答为a+b，
∴（a﹣b）2≤正方形MNPQ的面积≤（a+b）2．
