��Ŀ����
����Ŀ���Ķ����ϣ�����˼����С���ڽⷽ����![]() ʱ��������һ��������������Ľⷨ��
ʱ��������һ��������������Ľⷨ��
�⣺�����̢ڱ��Σ�4x+10y+y��5��2��2x+5y��+y��5�ۣ��ѷ��̢ٴ���۵ã�2��3+y��5��y����1����y����1����ٵ�x��4�����ԣ�������Ľ�Ϊ![]() ��
��
�������������⣺
��1��ģ��С������������������ⷽ����![]() ��
��
��2����֪x��y���㷽����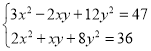 ����x2+4y2��xy��ֵ��
����x2+4y2��xy��ֵ��
���𰸡���1��![]() ����2��15.
����2��15.
��������
��1�������ó�3��2x��3y����2y��9���������������ó�15��2y��9�����y����y��3���������x���ɣ�
��2���������x2+4y2��![]() �����������������xy��2���������ó�x2��3xy+4y2��11����������𰸣�
�����������������xy��2���������ó�x2��3xy+4y2��11����������𰸣�
�⣺��1��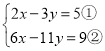
�ɢڵã�3��2x��3y����2y��9�ۣ�
�Ѣٴ���۵ã�15��2y��9��
��ã�y��3��
��y��3����ٵã�2x��9��5��
��ã�x��7��
����ԭ������Ľ�Ϊ![]() ��
��
��2��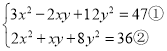
�ɢٵã�3��x2+4y2����2xy��47��
x2+4y2��![]() �ۣ�
�ۣ�
�Ѣ۴���ڵã�2��![]() +xy��36��
+xy��36��
��ã�xy��2��
�٩��ڵã�x2��3xy+4y2��11��
��x2+4y2��11+3��2��17��
��x2+4y2��xy��17��2��15��

��ϰ��ϵ�д�
 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д�
�����Ŀ