题目内容
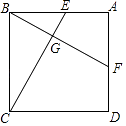
【题目】如图1,等腰△ABC中,AB=AC,∠BAC=30°,AB边上的中垂线DE分别交AB,AC于点D、E,∠BAC的平分线交DE于点F.连接BF、CF、BE.
(1)求证:△BCF为等边三角形;
(2)猜想EF、EB、EC三条线段的关系,并说明理由;
(3)如图2,在BE的延长线上取一点M,连接AM,使AM=AB,连接MC并延长交AF的延长线于点M.求证:AN=MC.

【答案】(1)详见解析;(2)BE=EF+EC,理由详见解析;(3)详见解析.
【解析】
(1)先根据角平分线定义得:∠BAF=∠CAF=15°,根据等腰三角形性质得:∠ABC=
∠ACB=75°,计算∠FBC=60°,由中垂线的性质得:AF=BF,证明△BAF≌△CAF(SAS),
可得BF=CF,根据有一个角是60°的等腰三角形是等边三角形,可得结论;
(2)如图1,作辅助线,构建等边三角形EFG,证明△BFG≌△CFE,可得BG=EC,可得:
BE=BG+EG=EF+EC;
(3)如图2,设AE=x,分别计算∠CAM=90°,∠NAH=60°,∠ANH=30°,可得![]()
![]() ,可得结论.
,可得结论.
证明:(1)如图1,∵∠BAC=30°,AF平分∠BAC,
∴∠BAF=∠CAF=15°,
∵AB=AC,
∴∠ABC=∠ACB=75°,
∵DE是AB的中垂线,
∴AF=BF,
∴∠BAF=∠ABF=15°,
∴∠FBC=75°﹣15°=60°,
在△BAF和△CAF中,
∵ 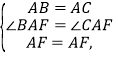
∴△BAF≌△CAF(SAS),
∴BF=CF,
∴△BCF是等边三角形;
(2)猜想:BE=EF+EC,
如图1,在BE上截取EF=FG,
∵DE是AB的中垂线,
∴AE=BE,
∴∠BED=∠AED=60°,
∴△FGE是等边三角形,
∴∠GFE=60°,EF=EG,
∵∠BFC=60°,
∴∠BFG=∠CFE,
在△BFG和△CFE中,
∵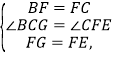
∴△BFG≌△CFE,
∴BG=EC,
∴BE=BG+EG=EF+EC;
(3)如图2,∵∠ABE=∠BAE=30°,
∴∠AEM=60°,
∵AB=AM,
∴∠ABE=∠AMB=30°,
∴∠EAM=90°,
设AE=x,则EM=2x,![]()
∵AB=AC=AM,
∴△ACM是等腰直角三角形,
∴![]()
∠AMC=45°,
过A作AH⊥MN于H,
∴△AMH是等腰直角三角形,
∴![]()
∵AC=AM,AH⊥CM,
∴∠CAH=45°,
∵∠NAC=![]() ∠BAC=15°,
∠BAC=15°,
∴∠NAH=15°+45°=60°,
∴∠ANH=30°,
∴![]()
∴AN=CM.

 阅读快车系列答案
阅读快车系列答案