题目内容
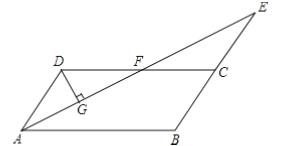
【题目】如图,在![]() ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且
ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且![]() ,连结
,连结![]() .
.

(1)求证:四边形![]() 是矩形;
是矩形;
(2)若CP=CD,AP=2,AD=6时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)证出∠A=90°即可;
(2)由HL证明Rt△CDQ≌Rt△CPQ,得出DQ=PQ,设AQ=x,则DQ=PQ=6-x,由勾股定理得出方程,解方程即可.
(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,
又∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形
∴∠D=∠CPQ=90°,在Rt△CDQ和Rt△CPQ中,![]() ,
,
∴Rt△CDQ≌Rt△CPQ(HL)),
∴DQ=PQ,
设AQ=x,则DQ=PQ=6-x
在Rt△APQ中,AQ2+AP2=PQ2
∴x2+22=(6-x)2,
解得:x=![]()
∴AQ的长是![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目