题目内容
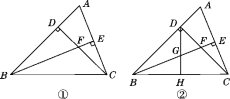
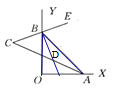
【题目】已知，如图，∠XOY=90°，点A、B分别在射线OX、OY上移动，BE是∠ABY的平分线，BE的反向延长线与∠OAB的平分线相交于点C，试问∠ACB的大小是否发生变化？如果保持不变，请给出证明；如果随点A、B移动发生变化，请求出变化范围．
【答案】∠ACB的大小不发生变化，且始终保持45°．
【解析】
【试题分析】
作∠ABO的平分线交AC于点D，则∠BDA＝180°-(∠DAB+∠DBA)＝180°-
(∠OAB+∠OBA)＝135°，由BD，BE分别是∠OBA和∠YBA的平分线，可知BD⊥CB，所以∠ACB＝∠BDA-∠DBC＝135°-90°＝45°．可见∠ACB的大小始终为45°．
【试题解析】
作∠ABO的平分线交AC于点D，则∠BDA＝180°-(∠DAB+∠DBA)＝180°- (∠OAB+∠OBA)＝135°，因为BD，BE分别是∠OBA和∠YBA的平分线，
所以BD⊥CB，所以∠ACB＝∠BDA-∠DBC＝135°-90°＝45°．
即∠ACB的大小始终为45°．
练习册系列答案
相关题目
【题目】小东根据学习函数的经验，对函数y= 
图象与性质进行了探究，下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数y= 的自变量x的取值范围是；
（2）如表是y与x的几组对应值．
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | | | | 2 | | 4 | | 2 | | | m | … |
表中m的值为；
（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出函数y= 的大致图象；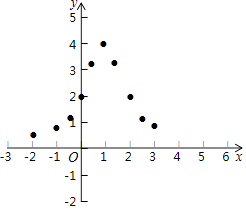 
（4）结合函数图象，请写出函数y= 
的一条性质.
（5）解决问题：如果函数y= 与直线y=a的交点有2个，那么a的取值范围是 ．
