题目内容
【题目】我们知道,直线与圆有三种位置关系:相交、相切、相离.类比直线与圆的位置关系,给出如下定义:与坐标轴不平行的直线与抛物线有两个公共点叫做直线与抛物线相交;直线与抛物线有唯一的公共点叫做直线与抛物线相切,这个公共点叫做切点;直线与抛物线没有公共点叫做直线与抛物线相离.
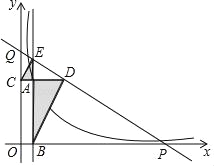
(1)记一次函数![]() 的图像为直线
的图像为直线![]() ,二次函数
,二次函数![]() 的图像为抛物线
的图像为抛物线![]() ,若直线
,若直线![]() 与抛物线
与抛物线![]() 相交,求
相交,求![]() 的取值范围;
的取值范围;
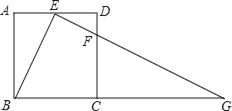
(2)若二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
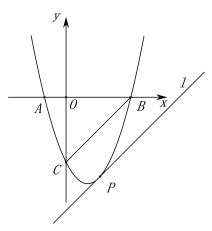
轴交于点![]() ,直线l与CB平行,并且与该二次函数的图像相切,求切点P的坐标.
,直线l与CB平行,并且与该二次函数的图像相切,求切点P的坐标.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)将一次函数解析式代入二次函数解析式中可得出关于x的一元二次方程,由直线与抛物线相交可得出关于b的一元一次不等式,解之即可得出b的取值范围;
(2)利用二次函数图象上点的坐标特征可得出点B,C的坐标,利用待定系数法可求出直线BC的解析式,设直线l的解析式为y=x+a,将一次函数解析式代入二次函数解析式中可得出关于x的一元二次方程,由直线与抛物线相切可得出关于a的一元一次方程,解之可得出a的值,解方程组即可求出点P的坐标.
(1)将y=2x+b代入y=x2,整理得:x2﹣2x﹣b=0.
∵直线l与抛物线C相交,∴△=(﹣2)2﹣4×1×(﹣b)>0,解得:b>﹣1.
(2)当x=0时,y=x2﹣2x﹣3=﹣3,∴点C的坐标为(0,﹣3);
当y=0时,x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,∴点A的坐标为(﹣1,0),点B的坐标为(3,0).
设直线BC的解析式为y=mx+n(m≠0),将B(3,0),C(0,﹣3)代入y=mx+n,得:![]() ,解得:
,解得:![]() ,∴直线BC的解析式为y=x﹣3.
,∴直线BC的解析式为y=x﹣3.
设直线l的解析式为y=x+a.
将y=x+a代入y=x2﹣2x﹣3,整理得:x2﹣3x﹣(3+a)=0.
∵直线l与二次函数y=x2﹣2x﹣3的图象相切,∴△=(﹣3)2﹣4×1×[﹣(3+a)]=0,解得:a![]() .
.
当a![]() 时,解方程组
时,解方程组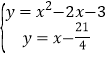 ,得:
,得: ,∴点P的坐标为(
,∴点P的坐标为(![]() ).
).