题目内容
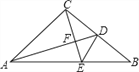
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过点C作AD的垂线,交AB于点F,求证∠ADC=∠BDE
【答案】见解析
【解析】试题分析:作CH⊥AB于H交AD于P,根据已知条件和等腰直角三角形的性质易证△APH≌△CEH,可得PH=EH,再证得CP=EB,∠PCD=∠EBD=45°,DC=DB,即可得△PDC≌△EDB,结论得证.
试题解析:
作CH⊥AB于H交AD于P,
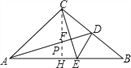
∵在Rt△ABC中,AC=CB,∠ACB=90°,
∴∠CAB=∠CBA=45.
∴∠HCB=90∠CBA=45=∠CBA.
又∵BC中点为D,
∴CD=BD.
又∵CH⊥AB,
∴CH=AH=BH.
又∵∠PAH+∠APH=90,∠PCF+∠CPF=90,∠APH=∠CPF,
∴∠PAH=∠ECH.
在△APH与△CEH中
∠PAH=∠ECH,AH=CH,∠PHA=∠EHC,
∴△APH≌△CEH(ASA).
∴PH=EH,
又∵PC=CHPH,BE=BHHE,
∴CP=EB.
∵△ACB是等腰直角三角形,
∴∠B=45,
即∠EBD=45,
∵CH⊥AB,
∴∠PCD=45=∠EBD,
在△PDC与△EDB中
PC=EB,∠PCD=∠EBD,DC=DB,
∴△PDC≌△EDB(SAS).
∴∠ADC=∠BDE.

练习册系列答案
相关题目