题目内容
【题目】已知二次函数y＝ax2（a≥1）的图像上两点A、B的横坐标分别是－1、2，点O是坐标原点，如果△AOB是直角三角形，则△OAB的周长为 ＿＿ 。
【答案】
【解析】利用勾股定理求得OA、OB、AB的长，再分别讨论以那一条边为斜边，进一步利用勾股定理解答即可．
解：如图，作AF⊥OD，BD⊥OF，AE⊥BD，
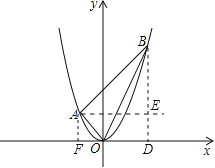
点A（-1，a），B（2，4a），由勾股定理得，
OA=
，
∵AE=1+2=3，BE=BD-DE=4a-a=3a，
AB=
，
因为a≥1，故OA边最小，不能为斜边；
（1）若OB为斜边，则OB2=OA2+AB2，
即4+16a2=a2+1+9+9a2，
解得a1=1，a2=-1（不合题意，舍去），
△AOB的周长=
（2）若AB为斜边，则AB2=OA2+OB2，
即9+9a2=a2+1+4+16a2，
解得a=±
（a≥1，不合题意，舍去）；
综上所知，△AOB的周长为（4
+2
）．
故填：（4
+2
）．
练习册系列答案
相关题目
