题目内容
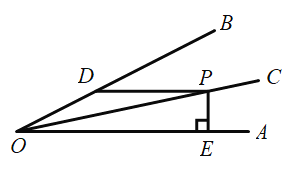
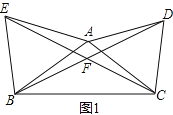
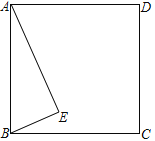
【题目】如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF
(1) 在图中画出点O和△CDF,并简要说明作图过程
(2) 若AE=12,AB=13,求EF的长
【答案】详见解析.
【解析】分析:(1)连接AC和BD,根据中心对称的性质可判断它们的交点为旋转中心O,延长EO到F,使FO=EO,则△CDF满足条件;
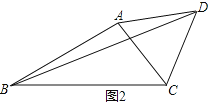
(2)过点O作OG⊥OE与EB的延长线交于点G,如图,先利用勾股定理计算出BE=5,再利用正方形的性质得OA=OB,∠AOB=90°,则∠AOE=∠BOG,接着根据三角形内角和得到∠GBO=∠EAO,于是可判断△EAO≌△GBO,所以AE=BG=12,OE=OG,然后判断△GEO为等腰直角三角形,则可得到OE=![]() EG=
EG=![]() (BG-BE)=
(BG-BE)=![]() ,从而得到EF=7
,从而得到EF=7![]() .
.
本题解析:
(1)连接 AC 和 BD ,则它们的交点为旋转中心 O ,延长 EO 到 F ,使 FO=EO ,
如图,点 O 和 △CDF 为所作;
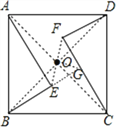
(2)过点 O 作 OG⊥OE 与 EB 的延长线交于点 G ,如图,
在 Rt△ABE 中 ,BE=![]() ,
,
∵ 四边形 ABCD 为正方形,
∴OA=OB,∠AOB=90°,
而 ∠EOG=90°,
∴∠AOE=∠BOG°,
∵∠AEB=∠AOB=90°,
∴∠GBO=∠EAO,
∴ 在 △EAO 和 △GBO 中,
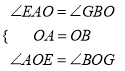 ,
,
∴△EAO ≌ △GBO ,
∴AE=BG=12, OE=OG ,
∴△GEO 为等腰直角三角形,
∴OE=![]() EG=
EG=![]() (BGBE)=
(BGBE)= ![]() ×(125)=
×(125)= ![]() ,
,
∴EF=2OE=7![]() .
.

练习册系列答案
相关题目