题目内容
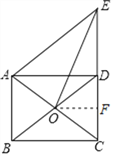
【题目】如图，矩形ABCD的对角线
相交于点O，过点A作BD的平行线交CD的延长线于点E．
求证： 
；
若
，连接OE，求
的值．
【答案】（1）证明见解析；（2）
【解析】试题分析：（1）根据矩形的对角线相等可得AC=BD，对边平行可得AB∥CD，再求出四边形ABDE是平行四边形，根据平行四边形的对边相等可得AE=BD，从而得证；
（2）如图，过点O作OF⊥CD于点F，欲求tan∠OEC的值，只需在直角△OEF中求得OF、FE的值即可．OF结合三角形中位线求得，EF结合矩形、平行四边形的性质以及勾股定理求得即可．
试题解析： 
四边形ABCD是矩形，
，
又
，
四边形ABDE是平行四边形，
，
；
如图，过点O作
于点F，
四边形ABCD是矩形，
．
，
．
同理，可得
，
．
在直角
中，由勾股定理可得： 
．
，
为
的中位线，
，
在直角
中， 
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
