��Ŀ����
����Ŀ�����Ķ����⣩����������ʵ��a��b��
��(![]() ��
��![]() )2��0��
)2��0��
��a��2![]() +b��0��
+b��0��
��a+b��2![]() ��(ֻ�е�a��bʱ��a+b����2
��(ֻ�е�a��bʱ��a+b����2![]() )��
)��
(1)����ý��ۣ���a+b��2![]() (a��b��Ϊ��ʵ��)�У���abΪ��ֵp��
(a��b��Ϊ��ʵ��)�У���abΪ��ֵp��
��a+b��2![]() ��ֻ�е�a��bʱ��a+b����Сֵ2
��ֻ�е�a��bʱ��a+b����Сֵ2![]() ��
��
�����������ݣ��ش��������⣺��m��0��ֻ�е�m���� ��ʱ��m+![]() ����Сֵ�� ����
����Сֵ�� ����
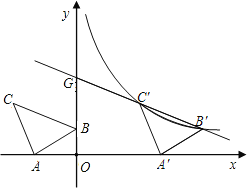
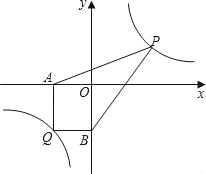
(2)��̽��Ӧ�ã���֪��Q(��3����4)��˫����y��![]() ��һ�㣬��Q��QA��x���ڵ�A����QB��y���ڵ�B����PΪ˫����y��
��һ�㣬��Q��QA��x���ڵ�A����QB��y���ڵ�B����PΪ˫����y��![]() (x��0)������һ�㣬����PA��PB�����ı���AQBP���������Сֵ��
(x��0)������һ�㣬����PA��PB�����ı���AQBP���������Сֵ��
���𰸡�(1)2��4��(2)24.
��������
��1�������IJ��Ͽɵã���m��![]() ʱ��m+
ʱ��m+![]() ȡ�����ֵ���ݴ˼�����⣻
ȡ�����ֵ���ݴ˼�����⣻
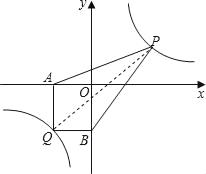
��2������PQ����P��x��![]() �������ݸ����ı���AQBP���������AQP�����+��QBP��������Ӷ�����x��ʾ���ı��ε�����������Ķ������н��ܵIJ���ʽ�����ʼ�����⣮
�������ݸ����ı���AQBP���������AQP�����+��QBP��������Ӷ�����x��ʾ���ı��ε�����������Ķ������н��ܵIJ���ʽ�����ʼ�����⣮
(1)��������õ�m��![]() ʱ��m��2����ʱm+
ʱ��m��2����ʱm+![]() ��4��
��4��
�ʴ��ǣ�2��4��
(2)����PQ����P(x��![]() )��
)��
��S�ı���AQBP��![]() ��4(x+3)+
��4(x+3)+![]() ��3(
��3(![]() +4)
+4)
��2x+![]() +12��12+12��24��
+12��12+12��24��
����СֵΪ24��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ