题目内容
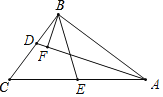
【题目】如图，在△ABC中，∠ABC＝90°，∠C＝52°，BE为AC边上的中线，AD平分∠BAC，交BC边于点D，过点B作BF⊥AD，垂足为F，则∠EBF的度数为( )
A.19°B.33°C.34°D.43°
【答案】B
【解析】
根据等边对等角和三角形内角和定理可得∠EBC＝52°，再根据角平分线的性质和垂直的性质可得∠FBD＝19°，最后根据∠EBF＝∠EBC﹣∠FBD求解即可．
解：∵∠ABC＝90°，BE为AC边上的中线，
∴∠BAC＝90°﹣∠C＝90°﹣52°＝38°，BE＝
AC＝AE＝CE，
∴∠EBC＝∠C＝52°，
∵AD平分∠BAC，
∴∠CAD＝∠BAC＝19°，
∴∠ADB＝∠C+∠DAC＝52°+19°＝71°，
∵BF⊥AD，
∴∠BFD＝90°，
∴∠FBD＝90°﹣∠ADB＝19°，
∴∠EBF＝∠EBC﹣∠FBD＝52°﹣19°＝33°；
故选：B．
练习册系列答案
相关题目
【题目】小明和小红为了更直观了解“物体质量”的概念，各选五个鸡蛋称重，以每个
为标准，大于或等于即为达标，超过标准部分的克数记为正数，不足标准部分的克数记为负数．小明所统计的数据为实际称重读数，小红为记录数据，把所得数据整理成如下统计表（单位：
）．
序号 数据 姓名 | 1 | 2 | 3 | 4 | 5 |
小明 | 48 | 50 |
| 49 | 51 |
小红 |
|
|
| 2 | 1 |
经过统计发现，小明所选鸡蛋质量的平均数为
，小红所选鸡蛋质量的众数为
，根据以上信息：
（1）填空：
，
；
（2）通过计算说明，小明和小红哪个选取的鸡蛋大小更均匀，请说明理由；
（3）现从小明和小红所选取的鸡蛋里各随机挑一个，这两个鸡蛋质量都达标的概率是多少？
