题目内容
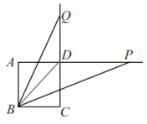
【题目】如图,正方形![]() 的边长为2,连接
的边长为2,连接![]() ,点
,点![]() 是线段
是线段![]() 延长线上的一个动点,
延长线上的一个动点,![]() ,点
,点![]() 是
是![]() 与线段
与线段![]() 延长线的交点,当
延长线的交点,当![]() 平分
平分![]() 时,
时,![]() ______
______![]() (填“>”“<”或“=”):当
(填“>”“<”或“=”):当![]() 不平分
不平分![]() 时,
时,![]() __________.
__________.
【答案】= 8
【解析】
①先证明△ABP≌△CBQ,再证明△QBD≌△PBD,即可得出PD=QD;②证明△BQD∽△PBD,即可利用对应边成比例求得PD·QD.
解:①当BD平分∠PBQ时,
∠PBQ=45°,
∴∠QBD=∠PBD=22.5°,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠C=90°,∠ABD=∠CBD=45°,
∴∠ABP=∠CBQ=22.5°+45°=67.5°,
在△ABP和△CBQ中,
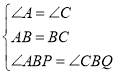
∴△ABP≌△CBQ(ASA),
∴BP=BQ,
在△QBD和△PBD中,
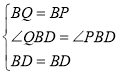
∴△QBD≌△PBD(SAS),
∴PD=QD;
②当BD不平分∠PBQ时,
∵AB∥CQ,
∴∠ABQ=∠CQB,
∵∠QBD+∠DBP=∠QBD+∠ABQ=45°,
∴∠DBP=∠ABQ=∠CQB,
∵∠BDQ=∠ADQ+∠ADB=90°+45°=135°,∠BDP=∠CDP+∠BDC=90°+45°=135°,
∴∠BDQ=∠BDP,
∴△BQD∽△PBD,
∴![]() ,
,
∴PD·QD=BD2=22+22=8,
故答案为:=,8.

练习册系列答案
相关题目