Question

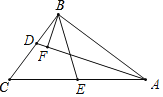
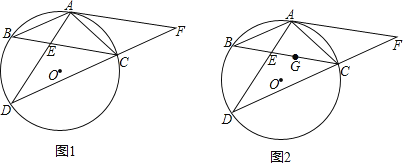
【题目】如图1，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，过点C作∠BCD＝∠ACB交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF＝AC，连接AF．

(1)求证：ED＝EC；

(2)求证：AF是⊙O的切线；

(3)如图2，若点G是△ACD的内心，BCBE＝25，求BG的长．

Answer 1

【答案】(1)见解析； (2)见解析； (3)5

【解析】

（1）根据AB＝AC，可得∠ABC＝∠ACB，再根据∠ACB＝∠BCD，∠ABC＝∠ADC，可得∠BCD＝∠ADC，根据等角对等边即可证明ED＝EC；

（2）连接OA，由垂径定理可得OA⊥BC，再通过角的和差关系可得∠CAF＝∠ACB，即可证明AF∥BC，即OA⊥AF，即可证明AF为⊙O的切线；

（3）连接AG，通过证明△ABE∽△CBA，可得＝，从而求得AB＝5，再根据点G为内心，可得∠DAG＝∠GAC，再根据∠BAD+∠DAG＝∠GAC+∠ACB，即可求出∠BAG＝∠BGA，根据等角对等边即可求出BG＝AB＝5．

解：（1）∵AB＝AC，

∴∠ABC＝∠ACB，

又∵∠ACB＝∠BCD，∠ABC＝∠ADC，

∴∠BCD＝∠ADC，

∴ED＝EC；

（2）如图1，连接OA，

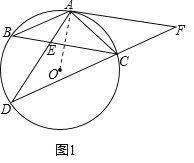
∵AB＝AC，

∴，

∴OA⊥BC，

∵CA＝CF，

∴∠CAF＝∠CFA，

∴∠ACD＝∠CAF+∠CFA＝2∠CAF，

∵∠ACB＝∠BCD，

∴∠ACD＝2∠ACB，

∴∠CAF＝∠ACB，

∴AF∥BC，

∴OA⊥AF，

∴AF为⊙O的切线；

（3）如图2，连接AG，

∵∠ABE＝∠CBA，∠BAD＝∠BCD＝∠ACB，

∴△ABE∽△CBA，

∴＝，

∴AB2＝BCBE，

∵BCBE＝25，

∴AB＝5，

∴∠BAG＝∠BAD+∠DAG，∠BGA＝∠GAC+∠ACB，

∵点G为内心，

∴∠DAG＝∠GAC，

又∵∠BAD+∠DAG＝∠GAC+∠ACB，

∴∠BAG＝∠BGA，

∴BG＝AB＝5．