题目内容
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 中点,以
中点,以![]() 为边作正方形
为边作正方形![]() ,边
,边![]() 交
交![]() 于点
于点![]() .在边
.在边![]() 上取点
上取点![]() 使
使![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
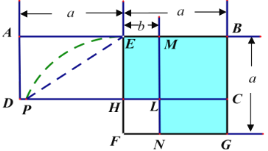
(1)请你利用该图解释平方差公式:![]() .
.
(2)现以点![]() 为圆心,
为圆心,![]() 为半径作圆弧交线段
为半径作圆弧交线段![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 在同一直线上,求
在同一直线上,求![]() 的值?
的值?
(3)记![]() 的面积为
的面积为![]() ,图中四边形
,图中四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)3;(3)![]()
【解析】
(1)分别利用a和b表示出S矩形ADLM和阴影部分的面积,然后根据S矩形ADLM=S矩形ADHE+S矩形EHLM =S矩形EHCB+S矩形LNGC=S阴影,即可证出结论;
(2)连接AG,利用平行证出△AML∽△GNL,然后列出比例式即可求出结论;
(3)连接PF,则PF=EF=a,HF=b,且a=3b,根据面积公式求出![]() 和
和![]() 即可求出结论.
即可求出结论.
解:(1)由图可知:AE=BE=BG=a,EM=b
由题已知:四边形ADLM、ADHE、EHCB、EHLM、LNGC都为矩形,四边形EFGB、HFNL都为正方形,CG=EM=b,BC=a-b且S矩形ADHE=S矩形EHCB,S矩形EHLM= S矩形LNGC
∴S矩形ADLM =AD·AM= BC·AM=(a-b)(a+b)
图中阴影部分的面积=S正方形EFGB-S正方形HFNL=a2-b2
∵S矩形ADLM=S矩形ADHE+S矩形EHLM =S矩形EHCB+S矩形LNGC=S阴影
∴(a-b)(a+b)= a2-b2
(2)连接AG,由题意可知,AG必过点L,
∵AM∥GN
∴△AML∽△GNL
∴![]()
即![]()
解得:a=3b
∴![]() =3;
=3;
(3)连接PF,则PF=EF=a,HF=b,且a=3b
∴PH=![]()
∴![]() =
=![]() PH·EH=
PH·EH=![]()
![]() ·(a-b)=
·(a-b)=![]()
![]() =a(a-b)=
=a(a-b)=![]()
∴![]() =
=![]()


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目