题目内容
2.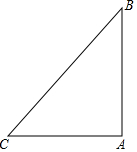 如图,已知△ABC中,∠BAC=90°,AB=AC,点D是△ABC内的一点,且AD=CD,BD=BA.
如图,已知△ABC中,∠BAC=90°,AB=AC,点D是△ABC内的一点,且AD=CD,BD=BA.(1)∠ABC=45°.
(2)依题中条件尺规作图补全图形.(不写作法,但保留作图痕迹)
(3)求∠CBD的角度.
分析 (1)根据等腰直角三角形的性质即可解决问题.
(2)作线段AC的垂直平分线MN,以B为圆心BA为半径画弧交MN于D,连接CD、AD、BD即可.
(3)作DM⊥AB于M,DN⊥AC于N.只要证明BD=2DM,推出∠ABD=30°即可解决问题.
解答 解:(1) ∵AC=AB,∠BAC=90°,
∵AC=AB,∠BAC=90°,
∴∠ABC=∠ACB=45°,
故答案为45°.
(2)如图所示,点D即为所求.
(3)作DM⊥AB于M,DN⊥AC于N.
∵∠DNA=∠NAM=∠DMA=90°,
∴四边形DNAM是矩形,
∴AN=DM,
∵DC=DA,DN⊥AC,
∴CN=AN=DN,
∵AC=AB=BD,
∴DM=$\frac{1}{2}$AC=$\frac{1}{2}$BD,
∴∠ABD=30°,
∴∠CBD=∠ABC-∠ABD=15°.
点评 本题考查作图-复杂作图、等腰直角三角形的性质、线段垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,记住直角三角形中,如果斜边等于直角边的两倍,这条直角边所对的锐角为30°,属于中考常考题型.

练习册系列答案
相关题目
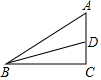 如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,且CD:AD=2:3,AC=10cm,则点D到AB的距离等于4cm.
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,且CD:AD=2:3,AC=10cm,则点D到AB的距离等于4cm. 在本次欧洲杯上有一精彩射门,如图所示,进攻队员站在点O处将足球从离地面0.5m的A处正对球门踢出(点A在y轴上).足球的飞行高度y(单位:m)与飞行时间i(单位:s)之间满足函数关系y=at2+5t+c.已知足球飞行1s时,离地面的高度为4m.
在本次欧洲杯上有一精彩射门,如图所示,进攻队员站在点O处将足球从离地面0.5m的A处正对球门踢出(点A在y轴上).足球的飞行高度y(单位:m)与飞行时间i(单位:s)之间满足函数关系y=at2+5t+c.已知足球飞行1s时,离地面的高度为4m. 有理数a、b、c在数轴上的位置如图,|a|-|a+b|-|c-a|+|b-c|=-a.
有理数a、b、c在数轴上的位置如图,|a|-|a+b|-|c-a|+|b-c|=-a.