题目内容
17.已知:b=$\sqrt{21×22×23×24+1}$-222,试完成下列计算(1-$\frac{a-b}{a+2b}$÷$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+4ab+4{b}^{2}}$)•(-$\frac{a}{2{b}^{2}}$-$\frac{1}{2b}$).分析 先将原式进行化简,然后求出b的值并代入求解即可.
解答 解:∵b=$\sqrt{21×22×23×24+1}$-222
=505-484
=21,
∴(1-$\frac{a-b}{a+2b}$÷$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+4ab+4{b}^{2}}$)•(-$\frac{a}{2{b}^{2}}$-$\frac{1}{2b}$)
=(1-$\frac{a-b}{a+2b}$÷$\frac{(a+b)(a-b)}{(a+2b)^{2}}$)•(-$\frac{a}{2{b}^{2}}$-$\frac{b}{2{b}^{2}}$)
=(1-$\frac{a+2b}{a+b}$)•(-$\frac{a+b}{2{b}^{2}}$)
=-$\frac{b}{a+b}$•(-$\frac{a+b}{2{b}^{2}}$)
=$\frac{1}{2b}$
=$\frac{1}{42}$.
点评 本题考查了分式的化简求值,解答本题的关键在于将原式进行化简,然后求出b的值并代入求解.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
6.下列语句正确的是( )
| A. | -b2的系数是1,次数是2 | B. | 2a+b是二次二项式 | ||
| C. | 多项式a2+ab-1是按照a的降幂排列 | D. | $\frac{2{a}^{2}b}{3}$的系数是2,次数是3 |
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 直角三角形 | B. | 线段 | C. | 角 | D. | 等腰梯形 |
 如图,已知△ABC中,∠BAC=90°,AB=AC,点D是△ABC内的一点,且AD=CD,BD=BA.
如图,已知△ABC中,∠BAC=90°,AB=AC,点D是△ABC内的一点,且AD=CD,BD=BA.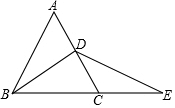 如图,D为AC上一点,E是BC延长线上一点,连接BD,DE,求证:∠ADB>∠CDE.
如图,D为AC上一点,E是BC延长线上一点,连接BD,DE,求证:∠ADB>∠CDE.