Question

【题目】如图，在正方形网格中，每个小正方形的边长为1，格点△ABC（顶点在网格线的交点上）的顶点A、C的坐标分别为A（﹣3，4）C（0，2）

（1）请在网格所在的平面内建立平面直角坐标系，并写出点B的坐标；

（2）画出△ABC关于原点对称的图形△A1B1C1；

（3）求△ABC的面积；

（4）在x轴上存在一点P，使PA+PB的值最小，请直接写出点P的坐标．

Answer 1

【答案】（1）坐标系详见解析，点B的坐标（﹣2，0）；（2）详见解析；（3）5；（4）点P的坐标（﹣2，0）．

【解析】

（1）根据A、C点坐标，作出的平面直角坐标系即可，根据作出的平面直角坐标系写出B点的坐标即可；
（2）根据原点对称的特点画出图形即可；
（3）利用矩形面积减去周围三角形面积得出即可；
（4）根据轴对称的性质解答即可．

解：（1）如图所示：

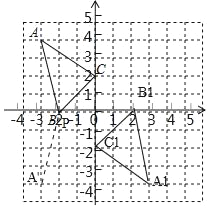
点B的坐标（-2，0）；

（2）如图所示，△A1B1C1即为所求；

（3）△ABC的面积=5；

（4）点P的坐标（-2，0）．