Question

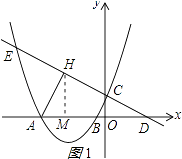
【题目】如图①，二次函数y=ax2﹣a（b﹣1）x﹣ab（其中b＜﹣1）的图象与x轴交于点A、B，与y轴交于点C（0，1），过点C的直线交x轴于点D（2，0），交抛物线于另一点E．

（1）用b的代数式表示a，则a=；
（2）过点A作直线CD的垂线AH，垂足为点H．若点H恰好在抛物线的对称轴上，求该二次函数的表达式；
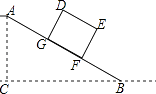
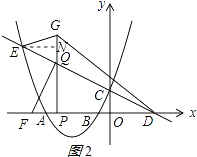
（3）如图②，在（2）的条件下，点P是x轴负半轴上的一个动点，OP=m．在点P左侧的x轴上取点F，使PF=1．过点P作PQ⊥x轴，交线段CE于点Q，延长线段PQ到点G，连接EG、DG．若tan∠GDP=tan∠FQP+tan∠QDP，试判断是否存在m的值，使△FPQ的面积和△EGQ的面积相等？若存在求出m的值，若不存在则说明理由．

Answer 1

【答案】
（1）解：∵二次函数y=ax2﹣a（b﹣1）x﹣ab（其中b＜﹣1），C（0，1），
∴﹣ab=1，
∴a=﹣ ；
故答案为：﹣
（2）

解：作HM⊥AD于M，如图1所示：

对称轴x=﹣ =﹣ = ，

设直线CD解析式为：y=kx+n，

∵C（0，1），D（2，0），

∴ ，

解得： ，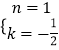

∴直线CD解析式为：y=﹣ +1，

H在对称轴上，将x= 代入y=﹣ +1，

y=﹣ +1= ，

∴H（ ， ），

由ax2﹣a（b﹣1）x﹣ab=0，则（ax+a）（x﹣b）=0，

∴x1=﹣1，x2=b，

∵b＜﹣1，

∴A（b，0），

HM= ，

AM=xM﹣xA= ﹣b=﹣ ，

DM=xD﹣xM=2﹣ = ，

由射影定理得：HM2=AMDM，

即（ ）2=﹣ ，

解得：b=﹣3，

∵a=﹣ ，

∴a= ，

∴y= x2﹣ （﹣3﹣1）x+1= x2+ x+1

（3）

解：存在m的值，使△FPQ的面积和△EGQ的面积相等；理由如下：

过点E作EN⊥GQ于点Q，如图2所示：

∵y= x2+ x+1与y=﹣ +1相交于点E，

∴ ，

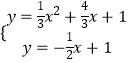解得：x=﹣ ，或x=0（不合题意舍去），y= ，

∴E（﹣ ， ），

∵PO=m，

∴xQ=﹣m，代入y=﹣ x+1得：yQ= m+1，

∵tan∠GDP= = = ，tan∠FQP= ，tan∠QDP= ，

∵tan∠GDP=tan∠FQP+tan∠QDP，

∴ ，

∴ ，

∵PD=m+2，PQ= m+1，PF=1，

∴ ，

解得：QG=2，

∵△FPQ的面积= PFPQ，△EGQ的面积= QGEN，△FPQ的面积和△EGQ的面积相等，EN= ﹣m，

∴ ×1×（ m+1）= ×2×（ ﹣m），

解得：m=4；

∴存在m的值，使△FPQ的面积和△EGQ的面积相等，m=4．

【解析】（1）将C（0，1）代入二次函数y=ax2﹣a（b﹣1）x﹣ab（其中b＜﹣1），得出﹣ab=1，即可得出结果；（2）作HM⊥AD于M，得出对称轴x=﹣ =﹣ = ，由C、D的坐标求出直线CD解析式为：y=﹣ +1，将x= 代入y=﹣ +1，得出H（ ， ），由ax2﹣a（b﹣1）x﹣ab=0，求出A（b，0），得出HM，AM，DM，由射影定理得：HM2=AMDM，解得b=﹣3，得出a= ，即可得出二次函数的表达式；（3）过点E作EN⊥GQ于点Q，由y= x2+ x+1与y=﹣ +1相交于点E，求出E（﹣ ， ），由PO=m，得出xQ=﹣m，yQ= m+1，由tan∠GDP= = ，tan∠FQP= ，tan∠QDP= img src="http://thumb.1010pic.com/questionBank/Upload/2017/07/19/20/0a7c1aa9/SYS201707192050383582795064_DA/SYS201707192050383582795064_DA.023.png" width="19" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ，得出 ，求出QG=2，再由△FPQ的面积= PFPQ，△EGQ的面积= QGEN，由△FPQ的面积和△EGQ的面积相等，得出方程，解方程即可．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．