题目内容
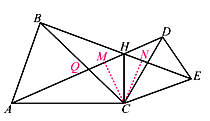
【题目】如图,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE交于点H,连接CH.
(1)求证:△ACD≌△BCE;
(2)求证:CH平分∠AHE;
(3)求∠CHE的度数.(用含α的式子表示)
【答案】(1)证明见解析;(2) 证明见解析;(3) 90°-![]() α
α
【解析】试题分析:(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS,即可判定:△ACD≌△BCE;
(2)首先作CM⊥AD于M,CN⊥BE于N,由△ACD≌△BCE,可证∠CAD=∠CBE,再证△ACM≌△BCN,(或证△ECN≌△DCM),可得CM=CN,即可证得CH平分∠AHE;
(3)由△ACD≌△BCE,可得∠CAD=∠CBE,继而求得∠AHB=∠ACB=α,则可求得∠CHE的度数.
试题解析:(1)证明:∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE.
在△ACD和△BCE中,

∴△ACD≌△BCE(SAS).
(2)证明:过点C作CM⊥AD于M,CN⊥BE于N.

∵△ACD≌△BCE,∴∠CAM=∠CBN.
在△ACM和△BCN中,

∴△ACM≌△BCN.
∴CM=CN.
∴CH平分∠AHE.
(3)令BC、AH交于点Q.
∵∠AQC=∠BQH,∠CAD=∠CBE,
∴∠AHB=∠ACB=α.
∴∠AHE=180°-α.
∴∠CHE=![]() ∠AHE=90°-
∠AHE=90°-![]() α.
α.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目

