题目内容
【题目】如图，△ABC中，∠A=50°，BD，CE是∠ABC，∠ACB的平分线，则∠BOC的度数为（ ）
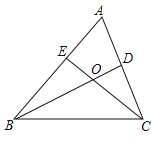
A.105°B.115°C.125°D.135°
【答案】B
【解析】
根据∠A=50°，可求出∠ABC+∠ACB的度数，再根据角平分线的定义得出∠OBC=
∠ABC，∠OCB=∠ACB，求出∠OBC+∠OCB的度数，根据三角形内角和定理求出即可．
∵∠A=50°，
∴∠ABC+∠ACB=180°∠A=130°，
∵BO、CO分别是△ABC中∠ABC、∠ACB的角平分线，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=(∠ABC+∠ACB)=65°，
∴∠BOC=180°(∠OBC+∠OCB)=180°65°=115°.
故选B.
练习册系列答案
相关题目
【题目】近年来网约车十分流行，初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查，司机月收入（单位：千元）如图所示：
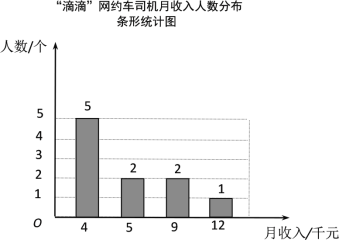
根据以上信息，整理分析数据如下：
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
（1）完成表格填空；
（2）若从两家公司中选择一家做网约车司机，你会选哪家公司，并说明理由．
