题目内容
【题目】如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．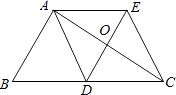 
（1）求证：AD=EC；
（2）当∠BAC=90°时，求证：四边形ADCE是菱形．
【答案】
（1）证明：∵DE∥AB，AE∥BC，
∴四边形ABDE是平行四边形，
∴AE∥BD，且AE=BD
又∵AD是BC边的中线，
∴BD=CD，
∴AE=CD，
∵AE∥CD，
∴四边形ADCE是平行四边形，
∴AD=EC
（2）证明：∵∠BAC=90°，AD是斜边BC上的中线，
∴AD=BD=CD，
又∵四边形ADCE是平行四边形，
∴四边形ADCE是菱形
【解析】（1）先证四边形ABDE是平行四边形，再证四边形ADCE是平行四边形，即得AD=CE；（2）由∠BAC=90°，AD是边BC上的中线，即得AD=BD=CD，证得四边形ADCE是平行四边形，即证；
练习册系列答案
相关题目
【题目】某校初一年级两个班的学生要到航天科普教育基地进行社会大课堂活动，两班学生共104人，其中初一（1）班有40多人，不足50人，教育基地门票价格如下：
购票张数 | 1～50张 | 51～100张 | 100张以上 |
每张票的价格 | 12元 | 10元 | 8元 |
原计划两班都以班为单位购票，则一共应付1240元，请回答下列问题：
（1）初一（1）班有多少人？
（2）你作为组织者如何购票最省钱？比原计划省多少钱？
【题目】某汽车行驶时油箱中余油量Q（L）与行驶时间t（h）的关系如表：
行驶时间t/h | 余油量Q/L |
1 | 42 |
2 | 34 |
3 | 26 |
4 | 18 |
5 | 10 |
（1）汽车行驶之前油箱中有汽油多少升？
（2）用行驶时间t的代数式表示余油量Q（直接写出答案）；
（3）当t＝
时，求余油量Q的值．
