Question

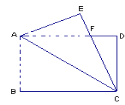
【题目】如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F.

（1）试说明：AF=FC；（2）如果AB=12，BC=16，求AF的长

Answer 1

【答案】（1）证明见解析；（2）12.5.

【解析】

（1）根据折叠的性质可得∠ACB=∠ACF，根据矩形的性质可得∠ACB=∠CAF，则即可得证；

（2）设AF=x，则DF=16﹣x，在Rt△CDF中，利用勾股定理得到关于x的方程，然后求解方程即可.

解：（1）∵四边形ABCD为矩形，△ABC与△AEC关于AC对称，

∴∠ACB=∠CAF，∠ACB=∠ACF，

∴∠CAF=∠ACF，

∴AF=FC；

（2）设AF=x，则DF=16﹣x，

在Rt△CDF中，CF2=DF2+CD2，

∴x2=（16﹣x）2+122，

解得x=12.5.